题目内容
(2012•芜湖三模)从1到20这20个正整数中,任取两个不同的整数,其和大于20的取法种数有( )
分析:根据题意,若每次取出2个数的和大于20,则两个数中至少有一个大于10,进而分两种情况讨论,①若取出的2个数都大于10,②若取出的2个数有一个小于或等于10,分别计算其所有的情况数目,进而由加法原理,计算可得答案.
解答:解:据题意,若每次取出2个数的和大于20,则两个数中至少有一个大于10,
可以分两种情况讨论,
①当取出的2个数都大于10时,则有
种.
②若取出的2个数有一个小于或等于10,
当一个数取1时,另1个只能取20,有C11种取法;
当一个数取2时,另1个只能取20或19,有C21种取法;
…
当一个数取10时,另1个数只能取20,19,18,…,11中的一个,有
种取法,
+1+2+3+…+10=100,
故选 B.
可以分两种情况讨论,
①当取出的2个数都大于10时,则有
| C | 2 10 |
②若取出的2个数有一个小于或等于10,
当一个数取1时,另1个只能取20,有C11种取法;
当一个数取2时,另1个只能取20或19,有C21种取法;
…
当一个数取10时,另1个数只能取20,19,18,…,11中的一个,有
| C | 1 10 |
| C | 2 10 |
故选 B.
点评:本题考查分类加法计数原理的运用,注意分类后,寻找规律,避免大量运算,其次注意分类讨论要不重不漏,属于中档题.

练习册系列答案
相关题目
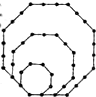 (2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是
(2012•芜湖三模)如图,将边长为1,2,3的正八边形叠放在一起,同一边上相邻珠子的距离为1,若以此方式再放置边长为4,5,6,…,10的正八边形,则这10个正八边形镶嵌的珠子总数是