题目内容
已知两圆相交于A(-1,3)、B(-6,m)两点,且这两圆的圆心均在直线x+y+c=0上,则点(m,c)不满足下列哪个方程( )
分析:由圆的性质可知,AB与x+y+c=0垂直且AB被x+y+c=0平分,可求KAB,从而可求m,然后由AB的中点在直线上可求c,结合选项可判断
解答: 解:由圆的性质可知,AB与x+y+c=0垂直且AB被x+y+c=0平分
解:由圆的性质可知,AB与x+y+c=0垂直且AB被x+y+c=0平分
∴KAB=
=
=1
∴m=-2
∵AB的中点在直线上
∴AB的中点(-
,
)即(-
,
)代入方程得c=3
(m,c)即为(-2,3)
结合选项可知(-2,3)满足x+2y=4,x+y=1,x2+y2=13
而2x+y=-1,故D不满足
故选D
 解:由圆的性质可知,AB与x+y+c=0垂直且AB被x+y+c=0平分
解:由圆的性质可知,AB与x+y+c=0垂直且AB被x+y+c=0平分∴KAB=
| m-3 |
| -6+1 |
| 3-m |
| 5 |
∴m=-2
∵AB的中点在直线上
∴AB的中点(-
| 7 |
| 2 |
| m+3 |
| 2 |
| 7 |
| 2 |
| 1 |
| 2 |
(m,c)即为(-2,3)
结合选项可知(-2,3)满足x+2y=4,x+y=1,x2+y2=13
而2x+y=-1,故D不满足
故选D
点评:本题主要考查了两圆相交性质:两圆的公共弦被连心线垂直平分的应用,属于基础试题

练习册系列答案
相关题目
 上,则点(m,c)不满足下列哪个方程( )
上,则点(m,c)不满足下列哪个方程( ) B.
B. C.
C. D.
D.
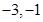 )两点,且两圆圆心都在直线
)两点,且两圆圆心都在直线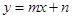 上,则
上,则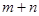 =
.
=
.