题目内容
直线l:2xsinα+2ycosα+1=0,圆C:x2+y2+2xsinα+2ycosα=0,l与C的位置关系是( )
| A.相交 | B.相切 | C.相离 | D.不能确定 |
圆C:x2+y2+2xsinα+2ycosα=0 即 (x+sinα)2+(y+cosα)2=1,
表示以C(-sinα-cosα)为圆心,半径等于1的圆.
圆心到直线的距离为d=
=1=r,故直线和圆相切,
故选:B.
表示以C(-sinα-cosα)为圆心,半径等于1的圆.
圆心到直线的距离为d=
| |-2sin2α-2cos2α| | ||
|
故选:B.

练习册系列答案
 星级口算天天练系列答案
星级口算天天练系列答案 芒果教辅达标测试卷系列答案
芒果教辅达标测试卷系列答案
相关题目
 :
: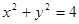 和
和 :
: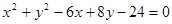 的位置关系是 .
的位置关系是 .