题目内容
(本小题满分12分)
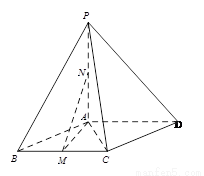
如图:在四棱锥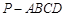 中,底面
中,底面 是菱形,
是菱形,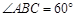 ,
,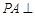 平面
平面 ,
,
点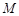 、
、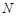 分别为
分别为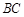 、
、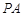 的中点,
的中点,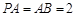 .
.
(I)证明: 平面
平面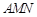 ;
;
(II)在线段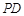 上是否存在一点
上是否存在一点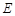 ,使得
,使得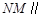 平面
平面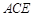 ;若存在,求出
;若存在,求出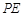 的长;若不存在,请说明理由。
的长;若不存在,请说明理由。
【答案】
(I)略
(II)
 平面
平面 ,即在
,即在 上存在一点
上存在一点 ,使得
,使得 平面
平面 ,
,
此时 .
.
【解析】解:(Ⅰ)因为 为菱形,所以
为菱形,所以
又 ,所以
,所以 ,
,
又 为
为 中点,所以
中点,所以
而 平面
平面 ,
, 平面
平面 ,所以
,所以
又 ,所以
,所以 平面
平面 (6分)
(6分)
(II)存在
取 中点
中点 ,连结
,连结 ,
, ,
, ,(8分)
,(8分)
因为 ,
, 分别为
分别为 、
、 中点,所以
中点,所以 且
且
又在菱形 中,
中, ,
,
所以 ,
, ,即
,即 是平行四边形
是平行四边形
所以 ,又
,又 平面
平面 ,
, 平面
平面
所以
 平面
平面 ,即在
,即在 上存在一点
上存在一点 ,使得
,使得 平面
平面 ,(10分)
,(10分)
此时 .(12分)
.(12分)

练习册系列答案
 名校联盟快乐课堂系列答案
名校联盟快乐课堂系列答案
相关题目