题目内容
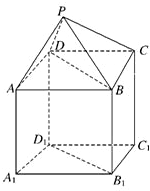
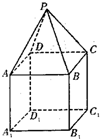 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=| 6 |
(1)求证:PA⊥B1D1;
(2)求平面PAD与平面BDD1B1所成的锐二面角θ的大小;
(3)求B1到平面PAD的距离.
分析:(1)连接AC,交BD于点O,连接PO,根据正四棱锥的几何特征易得PO⊥面ABCD,进而PO⊥BD,再由正方形对角线互相垂直得AC⊥BD,由线面垂直的判定定理可得BD⊥平面PAC,进而PA⊥BD,结合BD∥B1D1,即可得到PA⊥B1D1;
(2)过点O作OM⊥PD于点M,连接AM,由(1)中结论,可证得∠AMO就是二面角A-PD-O的平面角,解三角形AMO,即可得到平面PAD与平面BDD1B1所成的锐二面角θ的大小;
(3)分别取AD,BC中点E,F,作平面PEF,交底面于两点S,S1,交B1C1于点B2,过点B2作B2B3⊥PS于点B3,则B2B3⊥面PAD,即B2B3的长就是点B1到平面PAD的距离.
(2)过点O作OM⊥PD于点M,连接AM,由(1)中结论,可证得∠AMO就是二面角A-PD-O的平面角,解三角形AMO,即可得到平面PAD与平面BDD1B1所成的锐二面角θ的大小;
(3)分别取AD,BC中点E,F,作平面PEF,交底面于两点S,S1,交B1C1于点B2,过点B2作B2B3⊥PS于点B3,则B2B3⊥面PAD,即B2B3的长就是点B1到平面PAD的距离.
解答: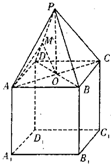 证明:(1)连接AC,交BD于点O,连接PO,
证明:(1)连接AC,交BD于点O,连接PO,
则PO⊥面ABCD,又∵AC⊥BD,
∴PA⊥BD,
∵BD∥B1D1,∴PA⊥B1D1.(4分)
解:(2)∵AO⊥BD,AO⊥PO,
∴AO⊥面PBD,
过点O作OM⊥PD于点M,连接AM,
则AM⊥PD,
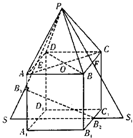 ∴∠AMO就是二面角A-PD-O的平面角,(6分)
∴∠AMO就是二面角A-PD-O的平面角,(6分)
又∵AB=2,PA=
,
∴OD=
,PO=
=2,
OM=
=
=
,
∴tan∠AMO=
=
=
,
即二面角的大小为arctan
.(8分)
(3)分别取AD,BC中点E,F,作平面PEF,交底面于两点S,S1,交B1C1于点B2,
过点B2作B2B3⊥PS于点B3,则B2B3⊥面PAD,又B1C1∥AD,
∴B2B3的长就是点B1到平面PAD的距离.(10分)
∵PO=AA1=2,
∴EF=
=2,tan∠PSS1=
=2,sin∠PSS1=
,
∴B2B3=B2Ssin∠PSS1=3×
=
.((12分) )
 证明:(1)连接AC,交BD于点O,连接PO,
证明:(1)连接AC,交BD于点O,连接PO,则PO⊥面ABCD,又∵AC⊥BD,
∴PA⊥BD,
∵BD∥B1D1,∴PA⊥B1D1.(4分)
解:(2)∵AO⊥BD,AO⊥PO,
∴AO⊥面PBD,
过点O作OM⊥PD于点M,连接AM,
则AM⊥PD,
 ∴∠AMO就是二面角A-PD-O的平面角,(6分)
∴∠AMO就是二面角A-PD-O的平面角,(6分)又∵AB=2,PA=
| 6 |
∴OD=
| 2 |
| 6-2 |
OM=
| PO•OD |
| PD |
2×
| ||
|
| 2 | ||
|
∴tan∠AMO=
| AO |
| OM |
| ||||
|
| ||
| 2 |
即二面角的大小为arctan
| ||
| 2 |
(3)分别取AD,BC中点E,F,作平面PEF,交底面于两点S,S1,交B1C1于点B2,
过点B2作B2B3⊥PS于点B3,则B2B3⊥面PAD,又B1C1∥AD,
∴B2B3的长就是点B1到平面PAD的距离.(10分)
∵PO=AA1=2,
∴EF=
| SS1 |
| 2 |
| 4 |
| 2 |
| 2 | ||
|
∴B2B3=B2Ssin∠PSS1=3×
| 2 | ||
|
6
| ||
| 5 |
点评:本题考查的知识点是二面角的平面角及求不地,空间点到平面的距离,直线与直线垂直的判定,其中(1)的关键是熟练掌握空间线线垂直,线面垂直的相互转化,(2)的关键是确定∠AMO就是二面角A-PD-O的平面角,(3)的关键是得到B2B3的长就是点B1到平面PAD的距离.

练习册系列答案
相关题目
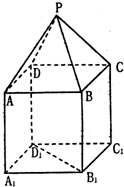 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=| 6 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA= 如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=
如图,P-ABCD是正四棱锥,ABCD-A1B1C1D1是正方体,其中AB=2,PA=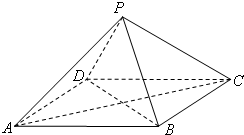 如图,P-ABCD是正四棱锥,
如图,P-ABCD是正四棱锥, 如图,P-ABCD是底面水平放置且△PAB在正面的正四棱锥,已知
如图,P-ABCD是底面水平放置且△PAB在正面的正四棱锥,已知