题目内容
如果复数
在复平面内的对应点在第二象限，则
A． | B． | C． | D． |
D
解析试题分析：根据复数的几何意义，由于复数在复平面内的对应点在第二象限，则实部为负数，虚部为正数，那么可知,故选D.
考点：复数的几何意义
点评：根据题意，由于复数的几何意义表示的为向量，利用实部和虚部的符号来确定，属于基础题。
练习册系列答案
相关题目
设
是虚数单位，复数
，则在复平面内
对应的点在 （ ）
| A．第一象限 | B．第二象限 | C．第三象限 | D．第四象限 |
若
是纯虚数，则实数
的值为（ ）
| A．1 | B． | C． | D．1或2 |
若
，其中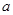
、
，
是虚数单位，则
| A．０ | B．２ | C． | D．５ |
设复数
的共轭复数为
，若
（
为虚数单位）则
( )
A． | B． | C． | D． |
复数
的虚部记作
，则
（ ）
A． | B． | C． | D． |
复数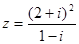
（i是虚数单位）在复平面上对应的点位于（ ）
| A．第一象限 | B．第二象限 |
| C．第三象限 | D．第四象限 |
已知复数
在复平面内对应的点分别为
，则
A． | B．  | C． | D． |
复数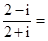
A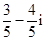． | B． | C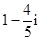． | D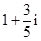． |