题目内容
【题目】已知抛物线![]() :
:![]() 的焦点为
的焦点为![]() ,平行于
,平行于![]() 轴的两条直线
轴的两条直线![]() ,
,![]() 分别交
分别交![]() 于
于![]() ,
,![]() 两点,交
两点,交![]() 的准线于
的准线于![]() ,
,![]() 两点.
两点.
(1)若![]() 在线段
在线段![]() 上,
上,![]() 是
是![]() 的中点,证明:
的中点,证明:![]() ;
;
(2)若△![]() 的面积是△
的面积是△![]() 的面积的两倍,求
的面积的两倍,求![]() 中点的轨迹方程.
中点的轨迹方程.
【答案】(1)证明见解析;(2)![]() .
.
【解析】
试题分析:(1)由题设![]() ,设
,设![]() :
:![]() ,
,![]() :
:![]() ,则
,则![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() ,利用斜率公式计算
,利用斜率公式计算![]() ;(2)由三角形面积关系得
;(2)由三角形面积关系得![]() ,再由当
,再由当![]() 与
与![]() 轴不垂直时,
轴不垂直时,![]() ,可得
,可得![]() (
(![]() )即
)即![]() ,检验
,检验![]() 与
与![]() 轴垂直时也成立.
轴垂直时也成立.
试题解析:由题设![]() ,设
,设![]() :
:![]() ,
,![]() :
:![]() ,则
,则![]() ,且
,且![]() ,
,![]() ,
,![]() ,
,![]() ,
,![]() .
.
记过![]() ,
,![]() 两点的直线为
两点的直线为![]() ,则
,则![]() 的方程为
的方程为![]() .
.
(1)由于![]() 在线段
在线段![]() 上,故
上,故![]() ,
,
记![]() 的斜率为
的斜率为![]() ,
,![]() 的斜率为
的斜率为![]() ,
,
则![]() ,
,
∴![]() .
.
(2)设![]() 与
与![]() 轴的交点为
轴的交点为![]() ,
,
则![]() ,
,![]() ,
,
由题设可得![]() ,
,
所以![]() (舍去),
(舍去),![]() .
.
设满足条件的![]() 的中点为
的中点为![]() ,
,
当![]() 与
与![]() 轴不垂直时,由
轴不垂直时,由![]() ,可得
,可得![]() (
(![]() ).
).
而![]() 所以
所以![]() (
(![]() ).
).
当![]() 与
与![]() 轴垂直时,
轴垂直时,![]() 与
与![]() 重合,
重合,
所以所求轨迹方程为![]() .
.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
【题目】某公司2016年前三个月的利润(单位:百万元)如下:
月份 |
|
|
|
利润 |
|
|
|
(1)求利润![]() 关于月份
关于月份![]() 的线性回归方程;
的线性回归方程;
(2)试用(1)中求得的回归方程预测![]() 月和
月和![]() 月的利润;
月的利润;
(3)试用(1)中求得的回归方程预测该公司2016年从几月份开始利润超过![]() 万?
万?
相关公式: 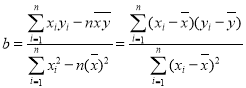 ,
, ![]() .
.