题目内容
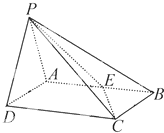 如图,在四棱锥P-ABCD中,侧面PAD是正三角形且与底面ABCD垂直,底面ABCD是矩形,E是AB中点,PC与平面ABCD的夹角为30°.
如图,在四棱锥P-ABCD中,侧面PAD是正三角形且与底面ABCD垂直,底面ABCD是矩形,E是AB中点,PC与平面ABCD的夹角为30°.
(1)求平面PCE与平面CED夹角的大小;
(2)当AD为多长时,点D到平面PCE的距离为2.
解:(1)取AD的中点O,连接PO.
∵△PAD是正三角形,∴PO⊥AD
∵面PAD⊥面ABCD,∴PO⊥面ABCD
以O为原点,过O作AB平行线为x轴,OD为y轴,OP为z轴建立空间直角坐标系,连OC,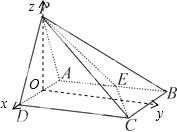
则∠PCO为PC与面ABCD所成角
∴∠PCO=30°
设AD=2a,则PO= a,∴OC=3a,∴CD=2
a,∴OC=3a,∴CD=2 a
a
∴P(0,0, a),C(2
a),C(2 a,a,0),E(
a,a,0),E( a,-a,0)
a,-a,0)
∴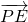 =(
=( a,-a,-
a,-a,- a),
a), =(2
=(2 a,a,-
a,a,- a),
a),
设平面PCE的法向量为 =(1,y,z),则
=(1,y,z),则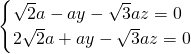
∴y= ,z=
,z= ,∴
,∴ =(1,
=(1, ,
, ),
),
又面DEC的法向量为 =(0,0,
=(0,0, a)
a)
∴cos<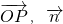 >=
>=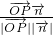 =
=
∴平面PCE与平面CED夹角的大小为45°
(2)∵D(0,a,0),∴ =(-2
=(-2 a,0,0)
a,0,0)
∴点D到平面PCE的距离为d= =
=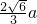
∵点D到平面PCE的距离为2
∴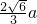 =2,∴a=
=2,∴a=
∴AD=2a= .
.
分析:(1)取AD的中点O,连接PO,则PO⊥面ABCD,以O为原点,过O作AB平行线为x轴,OD为y轴,OP为z轴建立空间直角坐标系,连OC.求出平面PCE的法向量、面DEC的法向量,利用向量的夹角公式,即可求平面PCE与平面CED夹角的大小;
(2)利用点D到平面PCE的距离为2,求出D的坐标,即可,求得AD的长.
点评:本题考查面面角,考查点到面的距离的计算,考查向量知识的运用,求得平面的法向量是关键.
∵△PAD是正三角形,∴PO⊥AD
∵面PAD⊥面ABCD,∴PO⊥面ABCD
以O为原点,过O作AB平行线为x轴,OD为y轴,OP为z轴建立空间直角坐标系,连OC,

则∠PCO为PC与面ABCD所成角
∴∠PCO=30°
设AD=2a,则PO=
 a,∴OC=3a,∴CD=2
a,∴OC=3a,∴CD=2 a
a∴P(0,0,
 a),C(2
a),C(2 a,a,0),E(
a,a,0),E( a,-a,0)
a,-a,0)∴
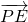 =(
=( a,-a,-
a,-a,- a),
a), =(2
=(2 a,a,-
a,a,- a),
a),设平面PCE的法向量为
 =(1,y,z),则
=(1,y,z),则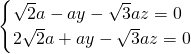
∴y=
 ,z=
,z= ,∴
,∴ =(1,
=(1, ,
, ),
),又面DEC的法向量为
 =(0,0,
=(0,0, a)
a)∴cos<
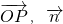 >=
>=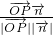 =
=
∴平面PCE与平面CED夹角的大小为45°
(2)∵D(0,a,0),∴
 =(-2
=(-2 a,0,0)
a,0,0)∴点D到平面PCE的距离为d=
 =
=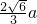
∵点D到平面PCE的距离为2
∴
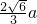 =2,∴a=
=2,∴a=
∴AD=2a=
 .
.分析:(1)取AD的中点O,连接PO,则PO⊥面ABCD,以O为原点,过O作AB平行线为x轴,OD为y轴,OP为z轴建立空间直角坐标系,连OC.求出平面PCE的法向量、面DEC的法向量,利用向量的夹角公式,即可求平面PCE与平面CED夹角的大小;
(2)利用点D到平面PCE的距离为2,求出D的坐标,即可,求得AD的长.
点评:本题考查面面角,考查点到面的距离的计算,考查向量知识的运用,求得平面的法向量是关键.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
 如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2
如图,在四棱锥P-ABCD中,底面ABCD是矩形.已知AB=3,AD=2,PA=2,PD=2 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,四边形ABCD为正方形,AB=4,PA=3,点A在PD上的射影为点G,点E在AB上,平面PEC⊥平面PDC. 如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a,
如图,在四棱锥P-ABCD中,PA⊥底面ABCD,∠BCD=120°,BC⊥AB,CD⊥AD,BC=CD=PA=a, 如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点
如图,在四棱锥P-ABCD中,底面是边长为a的菱形,∠ABC=60°PD⊥面ABCD,PC=a,E为PB中点 (2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.
(2008•武汉模拟)如图,在四棱锥P-ABCD中,底面ABCD是直角梯形,BC∥AD,且∠BAD=90°,又PA⊥底面ABCD,BC=AB=PA=1,AD=2.