题目内容
已知函数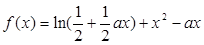
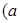 为常数,
为常数,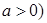
(1)当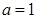 时,求函数
时,求函数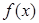 在
在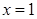 处的切线方程;
处的切线方程;
(2)当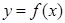 在
在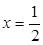 处取得极值时,若关于
处取得极值时,若关于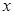 的方程
的方程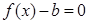 在
在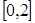 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;
(3)若对任意的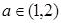 ,总存在
,总存在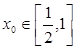 ,使不等式
,使不等式 成立,求实数
成立,求实数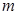 的取值范围。
的取值范围。
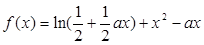
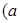 为常数,
为常数,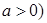
(1)当
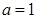 时,求函数
时,求函数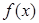 在
在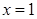 处的切线方程;
处的切线方程; (2)当
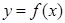 在
在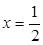 处取得极值时,若关于
处取得极值时,若关于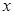 的方程
的方程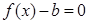 在
在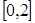 上恰有两个不相等的实数根,求实数
上恰有两个不相等的实数根,求实数 的取值范围;
的取值范围;(3)若对任意的
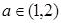 ,总存在
,总存在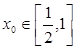 ,使不等式
,使不等式 成立,求实数
成立,求实数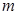 的取值范围。
的取值范围。(1) 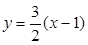 (2)
(2) 
(3)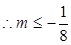
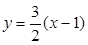 (2)
(2) 
(3)
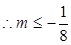
试题分析:(1)
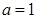 时,
时,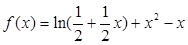
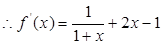 ,于是
,于是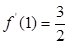 ,又
,又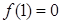 ,即切点为(
,即切点为(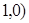
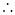 切线方程为
切线方程为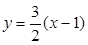 —————————————————————————5分
—————————————————————————5分(2)
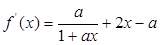 ,
,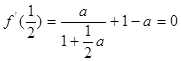 ,即
,即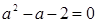 ,
,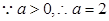
此时,
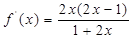 ,
,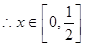 上减,
上减,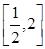 上增,
上增,又
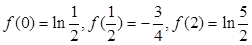
 ———————————————————————————10分
———————————————————————————10分(3)
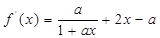
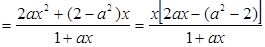
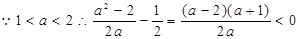 ,即
,即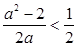 (
(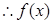 在
在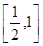 上增,
上增,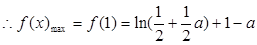
 只须
只须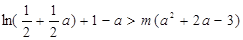 ————————————————12分
————————————————12分(法一)设
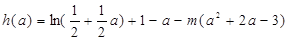
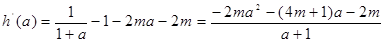
又
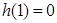
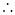
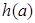 在1的右侧需先增,
在1的右侧需先增,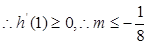
设
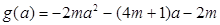 ,对称轴
,对称轴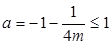
又
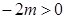 ,
,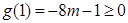
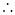 在
在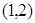 上,
上,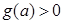 ,即
,即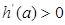
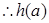 在
在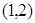 上单调递增,
上单调递增,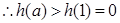
即
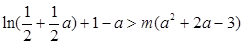 ,
,于是

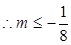 ——————————————————-15分
——————————————————-15分(法二)
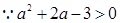
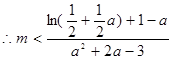
设
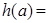
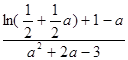 ,
,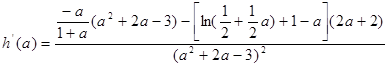
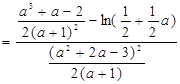
设
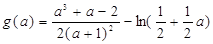 ,
,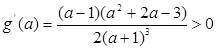
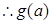 在
在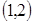 上增,又
上增,又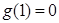 ,
,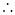
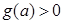 ,即
,即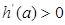 ,
,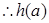 在
在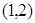 上增
上增又
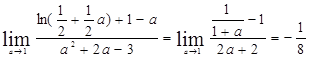
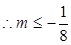
数学 选修1B模块答案
题号:03答案
(1)法一:由柯西不等式知:
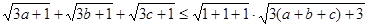
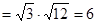 ——————————————————5分
——————————————————5分法二:
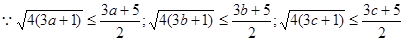
相加得:

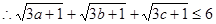 ——————————————————————5分
——————————————————————5分法三:令
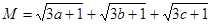
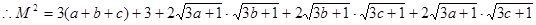
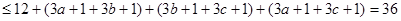
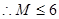 —————————————————————————————————5分
—————————————————————————————————5分(2)由柯西不等式得:
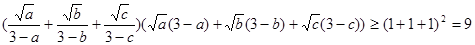
又
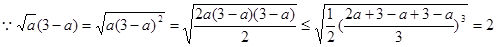
此时,
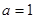 时取“=”号;同理:
时取“=”号;同理: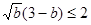 ,
,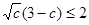 .
.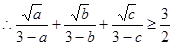 ,所以,当
,所以,当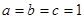 时,
时,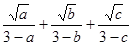 的最小值为
的最小值为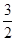
(提示:本题也可以用基本不等式求解:如:
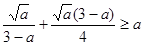 ,其中
,其中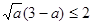 也可以构造函数
也可以构造函数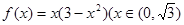 用导数求最大值)—————————10分
用导数求最大值)—————————10分题号:04答案
(1)直线
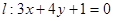
令
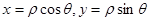 代入直线方程得:
代入直线方程得: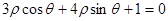
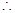 直线
直线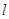 的极坐标方程为:
的极坐标方程为: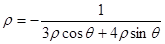 .————————————3分
.————————————3分(写成
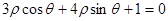 的形式不扣分)
的形式不扣分)(2)(i)曲线C的普通方程为:
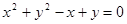 ————————————4分
————————————4分直线L的参数方程的标准形式为:
 ——————————————5分
——————————————5分联立得:
 ,
,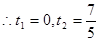 ;
;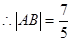 ———————————7分
———————————7分(ii)设AB中点为M对应的参数为
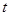 ,则
,则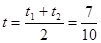 ,
,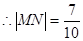 —————————————————————————————10分
—————————————————————————————10分点评:对于导数在研究函数中的问题,主要考查两个方面,一个是几何意义的运用,一个就是判定函数单调性,属于中档题。

练习册系列答案
相关题目
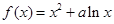 .
.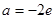 时,求函数
时,求函数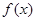 的单调区间和极值;
的单调区间和极值;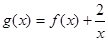 在区间
在区间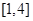 上是单调递减函数,求实数
上是单调递减函数,求实数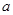 的取值范围.
的取值范围. 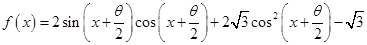
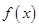 的最小正周期.
的最小正周期.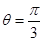 时,求函数
时,求函数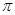 ]上是减函数的是
]上是减函数的是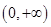 上为减函数的是( )
上为减函数的是( )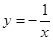
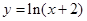
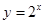
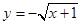
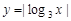 在区间
在区间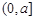 上单调递减,则实数
上单调递减,则实数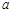 的取值范围为 .
的取值范围为 . 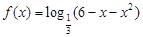 的单调递增区间是
的单调递增区间是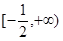
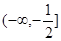
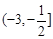
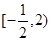
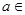 R,函数
R,函数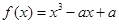 .
.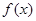 的单调区间;
的单调区间;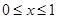 时,
时,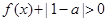 .
.


