题目内容
已知椭圆C的中心在原点,焦点在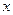 轴上,长轴长是短轴长的
轴上,长轴长是短轴长的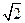 倍且经过点M
倍且经过点M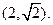
(Ⅰ)求椭圆C的方程
(Ⅱ)过圆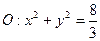 上的任一点作圆的一条切线交
上的任一点作圆的一条切线交 椭圆C与A、B两点
椭圆C与A、B两点
①求证: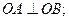
②求|AB|的取值范围
解:(Ⅰ)设椭圆的长半轴长为 ,短轴长为
,短轴长为 ,则由题意可得:
,则由题意可得: ,所以椭圆的方程为
,所以椭圆的方程为 ;
;
(Ⅱ)①当切线 的斜率不存在时切线为
的斜率不存在时切线为 与椭圆
与椭圆 的两个交点为
的两个交点为 或
或 满
满 足
足
当切线 斜率存在时,可设
斜率存在时,可设 的方程为
的方程为 .解方程组
.解方程组 得
得 ,即
,即 , w.w
, w.w .w.zxxk.c.o.m
.w.zxxk.c.o.m
则△= ,即
,即
 ,
,


②由①可知:



当 时
时
因为 所以
所以 ,
,
所以 ,
,
所以 当且仅当
当且仅当 时取”=”
时取”=”
当 时,
时, .
.
当AB的斜率不存在时, 两个交点为 或
或 ,所以此时
,所以此时 ,
,
综上, |AB |的取值范围为 即:
即: 
解析

练习册系列答案
 世纪百通主体课堂小学课时同步达标系列答案
世纪百通主体课堂小学课时同步达标系列答案 世纪百通优练测系列答案
世纪百通优练测系列答案 百分学生作业本题练王系列答案
百分学生作业本题练王系列答案
相关题目

 。
。