题目内容
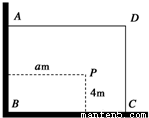
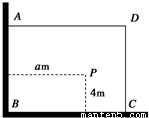
如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a米(0<a<12)、4米,不考虑树的粗细. 现在想用16米长的篱笆,借助墙角围成一个矩形的花圃ABCD, 并要求将这棵树围在花圃内或在花圃的边界上,设BC=x米,此矩形花圃的面积为y平方米。

(Ⅰ)写出y关于x的函数关系,并指出这个函数的定义域;
(Ⅱ)当BC为何值时,花圃面积最大?
(Ⅱ)当BC为何值时,花圃面积最大?
解:(Ⅰ)由已知AB=16-x,
∴ ,
,
又 ,
,
∴ ,
,
故函数定义域为[a,12]。
(Ⅱ)由 ,对称轴为x=8,
,对称轴为x=8,
又 ,
,
∴当 时,x=8,即BC=8米时,
时,x=8,即BC=8米时, ;
;
当 时,y在[a,12]上递减,
时,y在[a,12]上递减,
∴x=a,即BC=a米时, 。
。
∴
 ,
,又
 ,
,∴
 ,
,故函数定义域为[a,12]。
(Ⅱ)由
 ,对称轴为x=8,
,对称轴为x=8,又
 ,
,∴当
 时,x=8,即BC=8米时,
时,x=8,即BC=8米时, ;
;当
 时,y在[a,12]上递减,
时,y在[a,12]上递减,∴x=a,即BC=a米时,
 。
。
练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
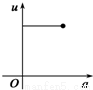
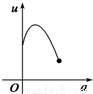
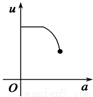
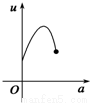
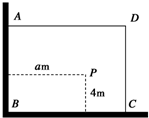 如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )
如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )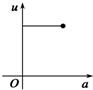
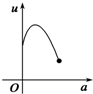
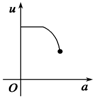
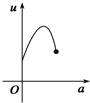
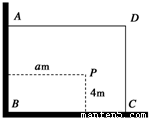 如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )
如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )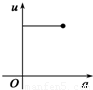
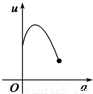

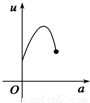
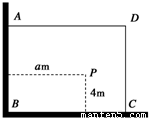 如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )
如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )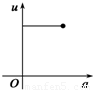
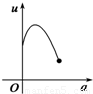
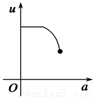
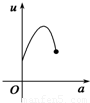
 如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )
如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )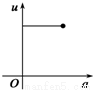
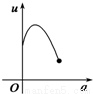
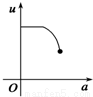
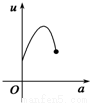
 如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )
如图,有一直角墙角,两边的长度足够长,在P处有一棵树与两墙的距离分别是a m(0<a<12)、4m,不考虑树的粗细.现在想用16m长的篱笆,借助墙角围成一个矩形的花圃ABCD.设此矩形花圃的最大面积为S,若将这棵树围在花圃内,则函数S=f(a)(单位m2)的图象大致是( )