题目内容
若直线2ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0所截得的弦长为4,则 的最小值为
的最小值为
- A.

- B.

- C.2
- D.4
D
分析:先求圆的圆心和半径,求弦心距,用弦心距、半径、半弦长的关系得到a、b 关系,来求 的最小值.
的最小值.
解答:圆x2+y2+2x-4y+1=0的圆心坐标(-1,2),半径是2,弦长是4,所以直线2ax-by+2=0(a>0,b>0)过圆心,
即:-2a-2b+2=0,∴a+b=1,将它代入 得,
得,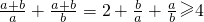 (因为a>0,b>0当且仅当a=b时等号成立).
(因为a>0,b>0当且仅当a=b时等号成立).
故选D.
点评:分析中用的是一般方法,解答中比较特殊,解题灵活,本题是一个好题目,学生容易受挫.
分析:先求圆的圆心和半径,求弦心距,用弦心距、半径、半弦长的关系得到a、b 关系,来求
 的最小值.
的最小值.解答:圆x2+y2+2x-4y+1=0的圆心坐标(-1,2),半径是2,弦长是4,所以直线2ax-by+2=0(a>0,b>0)过圆心,
即:-2a-2b+2=0,∴a+b=1,将它代入
 得,
得,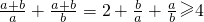 (因为a>0,b>0当且仅当a=b时等号成立).
(因为a>0,b>0当且仅当a=b时等号成立).故选D.
点评:分析中用的是一般方法,解答中比较特殊,解题灵活,本题是一个好题目,学生容易受挫.

练习册系列答案
 名校练考卷期末冲刺卷系列答案
名校练考卷期末冲刺卷系列答案
相关题目
若直线2ax-by+2=0(a>0,b>0)被圆x2+y2+2x-4y+1=0截得的弦长为4,则
+
的最小值是( )
| 1 |
| a |
| 2 |
| b |
A、4
| ||
B、3+2
| ||
C、3+2
| ||
D、4
|