��Ŀ����
��F1��F2�ֱ�Ϊ��ԲC��
+
=1��a��b��0���������������㣮
��1������ԲC�ϵĵ�A��1��
����F1��F2����ľ���֮�͵���4��д����ԲC�ķ��̺ͽ������ꣻ
��2�����K�ǣ�1����������Բ�ϵĶ��㣬���߶�F1K���е�Ĺ켣���̣�
��3����֪��Բ�������ʣ���M��N����ԲC�Ϲ���ԭ��ԳƵ������㣬��P����Բ������һ�㣬��ֱ��PM��PN��б�ʶ����ڣ�����ΪkPM��kPNʱ����ôkPM��kPN֮�������Pλ���صĶ�ֵ���Զ�˫����
-
=1д�������������Ե����ʣ�������֤����
| x2 |
| a2 |
| y2 |
| b2 |
��1������ԲC�ϵĵ�A��1��
| 3 |
| 2 |
��2�����K�ǣ�1����������Բ�ϵĶ��㣬���߶�F1K���е�Ĺ켣���̣�
��3����֪��Բ�������ʣ���M��N����ԲC�Ϲ���ԭ��ԳƵ������㣬��P����Բ������һ�㣬��ֱ��PM��PN��б�ʶ����ڣ�����ΪkPM��kPNʱ����ôkPM��kPN֮�������Pλ���صĶ�ֵ���Զ�˫����
| x2 |
| a2 |
| y2 |
| b2 |
��������1����ԲC�Ľ�����x���ϣ�����Բ�ϵĵ�A��F1��F2����ľ���֮����4��������Բ�Ķ���ɵ�2a=4����a=2�����õ�A��1��
������Բ�ϣ������b2=3���Ӷ�������ԲC�ķ��̣�
��2���������е����깫ʽ��ö�����F1K֮�������ϵ�����ö�������Բ�ϣ������е�Ĺ켣���̣�
��3�����M������Ϊ��m��n�������N������Ϊ��-m��-n����������֪
-
=1�������P������Ϊ��x��y������ʾ��ֱ��PM��PN��б�ʣ������ֱ��б�ʳ˻��ı���ʽ����y��x�ı���ʽ���뷢�ֽ����p�أ�
| 3 |
| 2 |
��2���������е����깫ʽ��ö�����F1K֮�������ϵ�����ö�������Բ�ϣ������е�Ĺ켣���̣�
��3�����M������Ϊ��m��n�������N������Ϊ��-m��-n����������֪
| m2 |
| a2 |
| n2 |
| b2 |
����⣺��1����ԲC�Ľ�����x���ϣ�����Բ�ϵĵ�A��F1��F2����ľ���֮����4����2a=4����a=2��
�ֵ�A��1��
������Բ�ϣ����b2=3������c2=1��
������ԲC�ķ���Ϊ
+
=1������F1��-1��0����F2��1��0����
��2������ԲC�ϵĶ���ΪK��x1��y1�����߶�F1K���е�Q��x��y������x1=2x+1��y1=2y��
���
+
=1����(x+
)2+
=1Ϊ����Ĺ켣���̣�
��3�����Ƶ�����Ϊ��MN��˫����
-
=1�Ϲ���ԭ��ԳƵ������㣬
��P��˫����������һ�㣬��ֱ��PM��PN��б�ʶ����ڣ�
����ΪkPM��kPNʱ����ôkPM��kPN֮�������Pλ���صĶ�ֵ��
���M��������m��n�������N��������-m��-n����
����
-
=1�������P��������x��y����
��kPM=
��kPN=
��
��kPM•kPN=
•
=
��
��y2=
x2-b2��n2=
m2-b2�������kPM•kPN=
��
�ֵ�A��1��
| 3 |
| 2 |
������ԲC�ķ���Ϊ
| x2 |
| 4 |
| y2 |
| 3 |
��2������ԲC�ϵĶ���ΪK��x1��y1�����߶�F1K���е�Q��x��y������x1=2x+1��y1=2y��
���
| (2x+1)2 |
| 4 |
| (2y)2 |
| 3 |
| 1 |
| 2 |
| 4y2 |
| 3 |
��3�����Ƶ�����Ϊ��MN��˫����
| x2 |
| a2 |
| y2 |
| b2 |
��P��˫����������һ�㣬��ֱ��PM��PN��б�ʶ����ڣ�
����ΪkPM��kPNʱ����ôkPM��kPN֮�������Pλ���صĶ�ֵ��
���M��������m��n�������N��������-m��-n����
����
| m2 |
| a2 |
| n2 |
| b2 |
��kPM=
| y-n |
| x-m |
| y+n |
| x+m |
��kPM•kPN=
| y-n |
| x-m |
| y+n |
| x+m |
| y2-n2 |
| x2-m2 |
��y2=
| b2 |
| a2 |
| b2 |
| a2 |
| b2 |
| a2 |
��������������ԲΪ���壬������Բ�ı����̣�������뷨��켣���̣�������Բ���ߵĹ�ͬ������������ѧ���ۺϷ�������ͽ�������������

��ϰ��ϵ�д�
 ��У����ϵ�д�
��У����ϵ�д�
�����Ŀ
 ��a��b��0���������������㣬��ԲC�ϵĵ�
��a��b��0���������������㣬��ԲC�ϵĵ�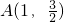 ������ľ���֮�͵���4��
������ľ���֮�͵���4�� ��|PQ|�����ֵ��
��|PQ|�����ֵ��