Question

正方体ABCD-A₁B₁C₁D₁的棱长为1，P、Q分别是正方形AA₁D₁D和A₁B₁C₁D₁的中心。

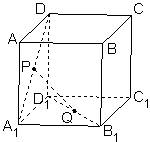
     （1）证明：PQ∥平面DD₁C₁C；

（2）求线段PQ的长；

（3）求PQ与平面AA₁D₁D所成的角。

Answer 1

证明：1）连接A₁C₁，DC₁，则Q为A₁C₁的中点

∴　PQ∥DC₁且PQ＝ DC₁

　    ∴　PQ∥平面DD₁C₁C

　　2）解：PQ＝ DC₁＝

　　3）解：∵　PQ∥DC₁　∴　PQ、DC₁与平面AA₁D₁D所成的角相等

∵　DC₁与平面AA₁D₁D所成的角为45°

　　∴　PQ与平面AA₁D₁D所成的角为45°.