题目内容
函数f(x)=log (x-1)+
(x-1)+ 的值域为________
的值域为________
[0,+∞)
分析:先求出函数的定义域,再利用函数的单调性求出函数的值域.
解答:由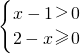 ,解得1<x≤2,
,解得1<x≤2,
∴函数f(x)的定义域为(1,2].
又∵函数y1=log (x-1)和y2=
(x-1)和y2= 在(1,2]上都是减函数,
在(1,2]上都是减函数,
∴当x=2时,f(x)有最小值,
f(2)=log (2-1)+
(2-1)+ =0,
=0,
f(x)无最大值,∴函数f(x)的值域为[0,+∞).
点评:本题考查函数的定义域和值域问题.
分析:先求出函数的定义域,再利用函数的单调性求出函数的值域.
解答:由
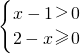 ,解得1<x≤2,
,解得1<x≤2,∴函数f(x)的定义域为(1,2].
又∵函数y1=log
 (x-1)和y2=
(x-1)和y2= 在(1,2]上都是减函数,
在(1,2]上都是减函数,∴当x=2时,f(x)有最小值,
f(2)=log
 (2-1)+
(2-1)+ =0,
=0,f(x)无最大值,∴函数f(x)的值域为[0,+∞).
点评:本题考查函数的定义域和值域问题.

练习册系列答案
相关题目
已知函数f(x)=log -
(x2-ax+3a)在[2,+∞)上是减函数,则实数a的范围是( )
| 1 |
| 2 |
| A、(-∞,4] |
| B、(-4,4] |
| C、(0,12) |
| D、(0,4] |