题目内容
解方程x4+1=0,并证明它的四个根为一个正方形的四个顶点.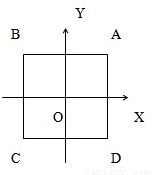
【答案】分析:将-1写为复数的三角形式,由方程的复数跟的表达式直接求出四个根,再由复数的几何意义找出复数在复平面内对应的点,进行证明即可.
解答:解:∵x4=-1=cosπ+isinπ,
∴x=cos ,k=0,1,2,3.
,k=0,1,2,3.
x1=cos .
.
x2=cos .
.
x3=cos .
.
x4=cos .
.
在复平面内(x为实轴,y为虚轴)
分别用A、B、C、D四点来表示四个根x1、x2、x3、x4(如图)
即A( ),B(-
),B(- ),
),
C(- ),D(
),D( )
)
∵A、B关于y轴对称,A、D关于x轴对称,∴∠A=90°,
同理,∠B=∠C=∠D=90°
且|AB|=|BC|=|CD|=|DA|= .
.
∴ABCD是正方形,而A、B、C、D是顶点.
点评:本题考查方程的复数跟的求解、复数的三角形式、复数的几何意义等知识,考查计算能力.
解答:解:∵x4=-1=cosπ+isinπ,
∴x=cos
 ,k=0,1,2,3.
,k=0,1,2,3.x1=cos
 .
.x2=cos
 .
.x3=cos
 .
.x4=cos
 .
.在复平面内(x为实轴,y为虚轴)
分别用A、B、C、D四点来表示四个根x1、x2、x3、x4(如图)
即A(
 ),B(-
),B(- ),
),C(-
 ),D(
),D( )
)∵A、B关于y轴对称,A、D关于x轴对称,∴∠A=90°,
同理,∠B=∠C=∠D=90°
且|AB|=|BC|=|CD|=|DA|=
 .
.∴ABCD是正方形,而A、B、C、D是顶点.
点评:本题考查方程的复数跟的求解、复数的三角形式、复数的几何意义等知识,考查计算能力.

练习册系列答案
相关题目
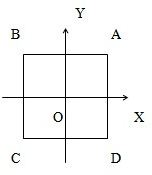 解方程x4+1=0,并证明它的四个根为一个正方形的四个顶点.
解方程x4+1=0,并证明它的四个根为一个正方形的四个顶点.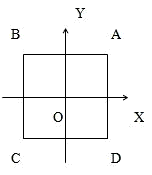
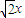 -1=0的解可视为函数y=x+
-1=0的解可视为函数y=x+ 的图象与函数y=
的图象与函数y=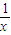 的图象交点的横坐标.若x4+ax-9=0的各个实根x1,x2,…,xk(k≤4)所对应的点
的图象交点的横坐标.若x4+ax-9=0的各个实根x1,x2,…,xk(k≤4)所对应的点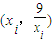 (i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是 .
(i=1,2,…,k)均在直线y=x的同侧,则实数a的取值范围是 .