题目内容
函数f（x）=2mcos2
+1的导函数的最大值等于1，则实数m的值为______．
| x |
| 2 |
f（x）=2mcos2
+1=2m×
+1=m+1+mcosx，
f（x）=-msinx
由于-1≤sinx≤1，
所以当m＞0时f（x）max=m=1，m=1
当m＜0时f（x）max=-m=1，m=-1
综上所述，m的值是1或-1
故答案为：1或-1
| x |
| 2 |
| 1+cosx |
| 2 |
f（x）=-msinx
由于-1≤sinx≤1，
所以当m＞0时f（x）max=m=1，m=1
当m＜0时f（x）max=-m=1，m=-1
综上所述，m的值是1或-1
故答案为：1或-1
练习册系列答案
阅读快车系列答案
相关题目
5、函数y=f（x）的图象如图所示，若∫0πf（x）dx=m，则∫02πf（x）dx等于（ ）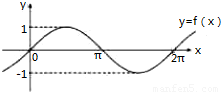
函数y=f（x）的图象如图所示，若
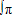f（x）dx=m，则
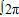f（x）dx等于（ ）
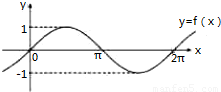函数y=f（x）的图象如图所示，若
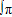f（x）dx=m，则
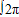f（x）dx等于（ ）