题目内容
15.已知实数x,y满足$\left\{\begin{array}{l}{x≥1}\\{x+y≤2}\\{x-y≤2}\end{array}\right.$,若不等式ax-y≤3恒成立,则实数a的取值范围为( )| A. | (-∞,4] | B. | (-∞,$\frac{3}{2}$] | C. | [$\frac{3}{2}$,2] | D. | [2,4] |
分析 作出不等式组对应的平面区域,利用线性规划的知识进行求解即可.
解答 解:作出不等式组对应的平面区域如图:
若ax-y≤3恒成立即y≥ax-3恒成立,
即平面区域ABC在直线y=ax-3的上方即可.
即C(2,0)在y=ax-3的上方或在直线上即可,
即2a≤3,解得a≤$\frac{3}{2}$,
故选:B
点评 本题主要考查线性规划的应用,根据条件ax-y≤3恒成立,得到平面区域ABC在直线y=ax-3的上方是解决本题的关键.

练习册系列答案
 目标测试系列答案
目标测试系列答案
相关题目
6.执行如图所示的程序框图,若P=$\frac{11}{12}$.则输出的n=( )


| A. | 4 | B. | 5 | C. | 6 | D. | 7 |
10.某全日制大学共有学生5400人,其中专科生有1500人,本科生有3000人,研究生有900人.现采用分层抽样的方法调查学生利用因特网查找学习资料的情况,抽取的样本为180人,则应在专科生、本科生与研究生这三类学生中分别抽取( )
| A. | 55人,80人,45人 | B. | 40人,100人,40人 | C. | 60人,60人,60人 | D. | 50人,100人,30人 |
4.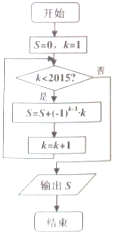 阅读如图所示的框图,运行相应的程序,则输出S的值为( )
阅读如图所示的框图,运行相应的程序,则输出S的值为( )
 阅读如图所示的框图,运行相应的程序,则输出S的值为( )
阅读如图所示的框图,运行相应的程序,则输出S的值为( )| A. | -1008 | B. | -1007 | C. | 1007 | D. | 1008 |