题目内容
设数列{an}满足a1=a,an+1=can+1-c(n∈N*),其中a,c为实数,且c≠0,
(Ⅰ)求证:a≠1时数列{an-1}是等比数列,并求an;
(Ⅱ)设a= ,c=
,c= ,bn=n(1-an)(n∈N*),求数列{bn}的前n项和Sn;
,bn=n(1-an)(n∈N*),求数列{bn}的前n项和Sn;
(Ⅲ)设 (n∈N*),记d2n=c2n-c2n-1(n∈N*),设数列{dn}的前n项和为Tn,求证:对任意正整数n都有Tn<
(n∈N*),记d2n=c2n-c2n-1(n∈N*),设数列{dn}的前n项和为Tn,求证:对任意正整数n都有Tn< 。
。
(Ⅰ)求证:a≠1时数列{an-1}是等比数列,并求an;
(Ⅱ)设a=
 ,c=
,c= ,bn=n(1-an)(n∈N*),求数列{bn}的前n项和Sn;
,bn=n(1-an)(n∈N*),求数列{bn}的前n项和Sn; (Ⅲ)设
 (n∈N*),记d2n=c2n-c2n-1(n∈N*),设数列{dn}的前n项和为Tn,求证:对任意正整数n都有Tn<
(n∈N*),记d2n=c2n-c2n-1(n∈N*),设数列{dn}的前n项和为Tn,求证:对任意正整数n都有Tn< 。
。 解:(Ⅰ)∵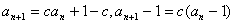 ,
,
a≠1时数列{an-1}是首项为a-1,公比为c的等比数列,
∴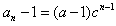 ,即
,即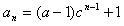 ;
;
(Ⅱ)由(Ⅰ)得,当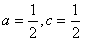 时,
时,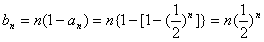 ,
,
∴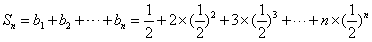 ,
,
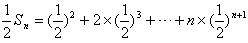 ,
,
两式作差得,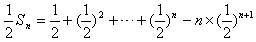 ,
,
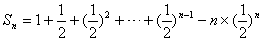
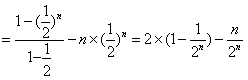 ,
,
∴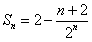 ;
;
(Ⅲ)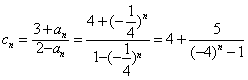 ,
,
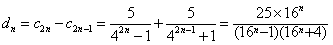
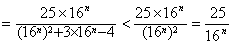 ,
,
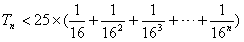
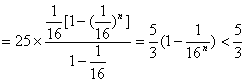 。
。
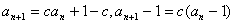 ,
,a≠1时数列{an-1}是首项为a-1,公比为c的等比数列,
∴
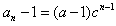 ,即
,即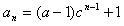 ;
;(Ⅱ)由(Ⅰ)得,当
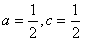 时,
时,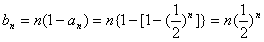 ,
,∴
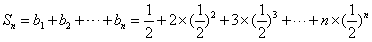 ,
,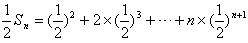 ,
,两式作差得,
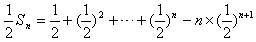 ,
,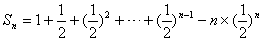
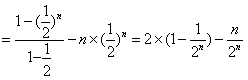 ,
,∴
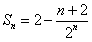 ;
;(Ⅲ)
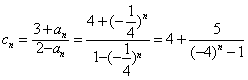 ,
,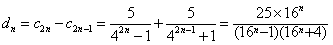
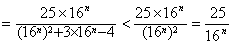 ,
,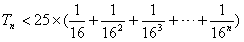
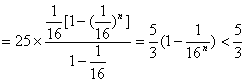 。
。 
练习册系列答案
 全程金卷系列答案
全程金卷系列答案 快乐5加2金卷系列答案
快乐5加2金卷系列答案
相关题目
设数列{an}满足a1=1,a2+a4=6,且对任意n∈N*,函数f(x)=(an-an+1+an+2)x+an+1?cosx-an+2sinx满足f′(
)=0若cn=an+
,则数列{cn}的前n项和Sn为( )
| π |
| 2 |
| 1 |
| 2an |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|