题目内容
7F直角边之和为12的直角三角形面积的最大值等于
- A.16
- B.18
- C.20
- D.不能确定
B
分析:设直角三角形的三边为:a.b.c,因为a+b=12,运用均值不等式即可求解ab的最大值,从而得出直角三角形面积的最大值.
解答:直角三角形的两直角边为a、b,面积为S,
 则a+b=12,
则a+b=12,
∴12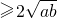
∴ab≤36
∴直角三角形面积S= ab≤18.
ab≤18.
故选B
点评:利用均值不等式解决实际问题时,列出有关量的函数关系式或方程式是均值不等式求解或转化的关键.
分析:设直角三角形的三边为:a.b.c,因为a+b=12,运用均值不等式即可求解ab的最大值,从而得出直角三角形面积的最大值.
解答:直角三角形的两直角边为a、b,面积为S,
 则a+b=12,
则a+b=12,∴12
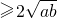
∴ab≤36
∴直角三角形面积S=
 ab≤18.
ab≤18.故选B
点评:利用均值不等式解决实际问题时,列出有关量的函数关系式或方程式是均值不等式求解或转化的关键.

练习册系列答案
相关题目