题目内容
已知函数f(x)=
单调递减,那么实数a的取值范围是( )
| A．(0,1) | B．(0, ) |
C．[ ,) | D．[,1) |
C
解析
练习册系列答案
轻松暑假总复习系列答案
相关题目
设
是集合M到集合N的映射, 若N="{1,2}," 则M不可能是 （ ）
| A．{－1} | B． | C． | D． |
已知偶函数f(x)当x∈[0，＋∞)时是单调递增函数，则满足f(
)＜f(x)的x的取值范围是( )
| A．(2，＋∞) | B．(－∞，－1) |
| C．[－2，－1)∪(2，＋∞) | D．(－1,2) |
定义在R上的函数y=f(x+1)的图象如图所示,它在定义域上是减函数,给出如下命题:①f(0)=1;②f(-1)=1;③若x>0,则f(x)<0;④若x<0,则f(x)>0,其中正确的是( )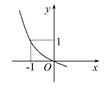
| A．②③ | B．①④ | C．②④ | D．①③ |
对于函数f(x)=acosx+bx2+c,其中a,b,c∈R,适当地选取a,b,c的一组值计算f(1)和f(-1),所得出的正确结果只可能是( )
| A．4和6 | B．3和-3 |
| C．2和4 | D．1和1 |
函数f(x)=
(x≠-
)满足f(f(x))=x,则常数c等于( )
| A．3 | B．-3 |
| C．3或-3 | D．5或-3 |
已知函数f(x)为奇函数，且当x>0时， f(x) ＝x2＋
，则f(－1)＝( )
| A．－2 | B．0 |
| C．1 | D．2 |
已知函数y=f(x+1)的定义域是[-2,3],则y=f(2x-1)的定义域是( )
A．[0, ] | B．[-1,4] |
| C．[-5,5] | D．[-3,7] |
x为实数，[x]表示不超过x的最大整数，则函数f(x)＝x－[x]在R上为( )
| A．奇函数 | B．偶函数 | C．增函数 | D．周期函数 |