题目内容
已知一扇形的面积S为定值,求当扇形的圆心角为多大时,它的周长最小?最小值是多少?
解:设半径是r,圆心角是θ
则S=
θ=
周长=2r+rθ=2r+ ≥4
≥4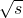
当2r=
即r2=S时取等号,此时θ= =2
=2
∴当扇形的圆心角为2rad时,
它的周长最小,最小值是4 .
.
分析:设出半径和圆心角,根据扇形的面积公式写出θ的表示式,根据扇形的周长包括两个半径和一个弧长,把角的表示式代入,利用基本不等式得到最小值,并求出取到最小值时的圆心角.
点评:本题考查扇形的面积公式,考查利用基本不等式求函数的最小值,考查扇形的面积,扇形的弧长和扇形的圆心角之间的关系,是一个综合题目.
则S=

θ=

周长=2r+rθ=2r+
 ≥4
≥4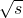
当2r=

即r2=S时取等号,此时θ=
 =2
=2∴当扇形的圆心角为2rad时,
它的周长最小,最小值是4
 .
.分析:设出半径和圆心角,根据扇形的面积公式写出θ的表示式,根据扇形的周长包括两个半径和一个弧长,把角的表示式代入,利用基本不等式得到最小值,并求出取到最小值时的圆心角.
点评:本题考查扇形的面积公式,考查利用基本不等式求函数的最小值,考查扇形的面积,扇形的弧长和扇形的圆心角之间的关系,是一个综合题目.

练习册系列答案
相关题目
 Rl,其中R为扇形半径,l为弧长)
Rl,其中R为扇形半径,l为弧长)