Question

已知等比数列{a_n}，若a₁+a₂+a₃=7，a₁a₂a₃=8,求a_n.

Answer 1

解法一：∵a₁a₃=a₂²，∴a₁a₂a₃=a₂³=8.

∴a₂=2.

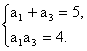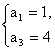从而解之，得或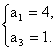

当a₁=1时，q=2；当a₁=4时，q=.

故a_n=2^n-1或a_n=2^3-n.

解法二：由等比数列的定义知a₂=a₁q,a₃=a₁q²代入已知得

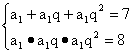
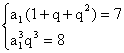
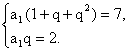
将a₁=代入得2q²-5q+2=0.

∴q=2或q=.

从而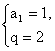或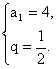

故a_n=2^n-1或a_n=2^3-n.

解法三：由等比数列的概念知a₁=,a₃=a₂q²,

代入a₁a₂a₃=8得a₂=2，

∴a₁=,a₃=2q.

代入a₁+a₂+a₃=7得+2+2q=7，解得q=2或q=.

当q=2时，a₁=1；当q=时，a₁=4.

故a_n=2^n-1或a_n=2^3-n.