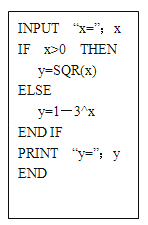题目内容
【题目】已知圆M：x2+（y﹣2）2=r2（r＞0）与曲线C：（y﹣2）（3x﹣4y+3）=0有三个不同的交点．
（1）求圆M的方程；
（2）已知点Q是x轴上的动点，QA，QB分别切圆M于A，B两点． ①若 
，求|MQ|及直线MQ的方程；
②求证：直线AB恒过定点．
【答案】
（1）解：因为直线3x﹣4y+3=0与圆M相切，
故圆心（0，2）到直线的距离为r，即： 
，r=1．
所以圆的方程为x2+（y﹣2）2=1．
（2）解：①设直线MQ，AB交于点P，则 
，
又|AM|=1，所以 
，
而|AM|2=|MP||MQ|，所以|MQ|=3，
设Q（x0，0），而点M（0，2），由 
， 
，
则 
或 
，
从而直线MQ的方程为： 
或 
．
②证明：设点Q（q，0），由几何性质可以知道，A，B在以MQ为直径的圆上，
此圆的方程为x2+y2﹣qx﹣2y=0，AB为两圆的公共弦，
两圆方程相减得qx﹣2y+3=0，
即 
，
所以过定点 
．
【解析】（1）因为直线3x﹣4y+3=0与圆M相切，圆心（0，2）到直线的距离为r，即可求圆M的方程；（2）①|AM|2=|MP||MQ|，所以|MQ|=3，求出Q的坐标，即可求出直线MQ的方程；②求出直线AB的方程，即可证明直线AB恒过定点．
练习册系列答案
培优好卷单元加期末卷系列答案
相关题目
