题目内容
给出下列命题:
(1)在△ABC中,“A<B”是”sinA<sinB”的充要条件;
(2)在同一坐标系中,函数y=sinx的图象和函数y=x的图象有三个公共点;
(3)在△ABC中,若AB=2,AC=3,∠ABC= ,则△ABC必为锐角三角形;
,则△ABC必为锐角三角形;
(4)将函数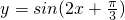 的图象向右平移
的图象向右平移 个单位,得到函数y=sin2x的图象,
个单位,得到函数y=sin2x的图象,
其中真命题的序号是 ________(写出所有正确命题的序号).
解:(1)sinA-sinB=2cos sin
sin
∵ <
< ,A<B
,A<B
∵2cos sin
sin <0
<0
进而可推断出,“A<B”是”sinA<sinB”的充要条件;(1)正确.
(2)根据正弦函数和直线的图象可知只有2个交点,(2)错误.
(3)由正弦定理可得 =
= ,求得sinA=
,求得sinA= ,若A为钝角,sinA=
,若A为钝角,sinA= <
< ,则A>
,则A> ,则A+B>π不符合题意,
,则A+B>π不符合题意,
故A只能为锐角.(3)正确.
(4)将函数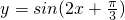 的图象向右平移
的图象向右平移 个单位得y=sin[2(x-
个单位得y=sin[2(x- )+
)+ ]=sin(2x-
]=sin(2x- )的图象,故(4)错误.
)的图象,故(4)错误.
故答案为:(1)(3).
分析:(1)通过利用和差化积公式判断出sinA-sinB与0的关系,进而可推断出(1)正确.
(2)通过正弦函数和直线的图象推断出(2)不正确.
(3)利用正弦定理求得sinA的值,假设为钝角通过正弦函数的单调性判断出A不符合,推断出A为锐角.(3)正确.
(4)利用三角函数图象变换的性质推断出(4)不正确.
点评:本题主要考查了三角函数的基本性质.综合考查了基础知识的熟练程度.
 sin
sin
∵
 <
< ,A<B
,A<B∵2cos
 sin
sin <0
<0进而可推断出,“A<B”是”sinA<sinB”的充要条件;(1)正确.
(2)根据正弦函数和直线的图象可知只有2个交点,(2)错误.
(3)由正弦定理可得
 =
= ,求得sinA=
,求得sinA= ,若A为钝角,sinA=
,若A为钝角,sinA= <
< ,则A>
,则A> ,则A+B>π不符合题意,
,则A+B>π不符合题意,故A只能为锐角.(3)正确.
(4)将函数
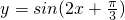 的图象向右平移
的图象向右平移 个单位得y=sin[2(x-
个单位得y=sin[2(x- )+
)+ ]=sin(2x-
]=sin(2x- )的图象,故(4)错误.
)的图象,故(4)错误.故答案为:(1)(3).
分析:(1)通过利用和差化积公式判断出sinA-sinB与0的关系,进而可推断出(1)正确.
(2)通过正弦函数和直线的图象推断出(2)不正确.
(3)利用正弦定理求得sinA的值,假设为钝角通过正弦函数的单调性判断出A不符合,推断出A为锐角.(3)正确.
(4)利用三角函数图象变换的性质推断出(4)不正确.
点评:本题主要考查了三角函数的基本性质.综合考查了基础知识的熟练程度.

练习册系列答案
相关题目