题目内容
已知f(x)=ax-ln(-x),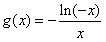 ,其中x∈[-e,0),e是自然常数,a∈R,
,其中x∈[-e,0),e是自然常数,a∈R,
(Ⅰ)讨论a=-1时,f(x)的单调性、极值;
(Ⅱ)求证:在(Ⅰ)的条件下,|f(x)|>g(x)+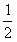 ;
;
(Ⅲ)是否存在实数a,使f(x)的最小值是3?如果存在,求出a的值;如果不存在,说明理由。
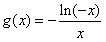 ,其中x∈[-e,0),e是自然常数,a∈R,
,其中x∈[-e,0),e是自然常数,a∈R, (Ⅰ)讨论a=-1时,f(x)的单调性、极值;
(Ⅱ)求证:在(Ⅰ)的条件下,|f(x)|>g(x)+
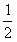 ;
;(Ⅲ)是否存在实数a,使f(x)的最小值是3?如果存在,求出a的值;如果不存在,说明理由。
(Ⅰ)解:∵f(x)=-x-ln(-x),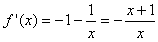 ,
,
∴当-e≤x<-1时,f′(x)<0,此时f(x)为单调递减;
当-1<x<0时,f′(x)>0,此时f(x)为单调递增,
∴f(x)的极小值为f(-1)=1.
(Ⅱ)证明:∵f(x)的极小值,即f(x)在[-e,0)的最小值为1,
∴|f(x)|min=1,
令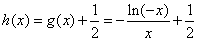 ,
,
又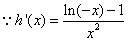 ,
,
当-e≤x<0时,h′(x)≤0,h(x)在[-e,0)上单调递减,
∴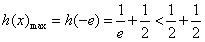 =1=|f(x)|min,
=1=|f(x)|min,
∴当x∈[-e,0)时,|f(x)|>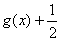 ;
;
(Ⅲ)解:假设存在实数a,使f(x)=ax-ln(-x)有最小值3,x∈[-e,0),
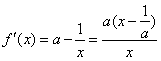 ,
,
①当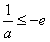 ,即
,即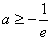 时,由于x∈[-e,0),则f′(x)=
时,由于x∈[-e,0),则f′(x)=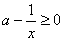 ,
,
∴函数f(x)=ax-ln(-x)是[-e,0)上的增函数,
∴f(x)min=f(-e)=-ae-1=3,解得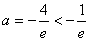 (舍去);
(舍去);
②当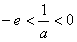 即
即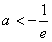 时,则当
时,则当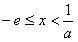 时,f′(x)=
时,f′(x)=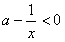 ,
,
此时f(x)=ax-ln(-x)是减函数;
当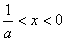 时,f′(x)=
时,f′(x)=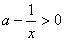 ,
,
此时f(x)=ax-ln(-x)是增函数,
∴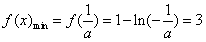 ,解得a=-e2,符合
,解得a=-e2,符合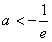 ;
;
③当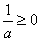 时,则f′(x)=
时,则f′(x)=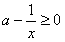 ,
,
∴函数f(x)=ax-ln(-x)是[-e,0)上的增函数,
∴f(x)min=f(-e)=-ae-1=3,解得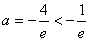 (舍去);
(舍去);
综上所述存在实数a=-e2.
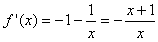 ,
,∴当-e≤x<-1时,f′(x)<0,此时f(x)为单调递减;
当-1<x<0时,f′(x)>0,此时f(x)为单调递增,
∴f(x)的极小值为f(-1)=1.
(Ⅱ)证明:∵f(x)的极小值,即f(x)在[-e,0)的最小值为1,
∴|f(x)|min=1,
令
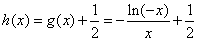 ,
,又
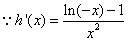 ,
,当-e≤x<0时,h′(x)≤0,h(x)在[-e,0)上单调递减,
∴
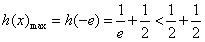 =1=|f(x)|min,
=1=|f(x)|min,∴当x∈[-e,0)时,|f(x)|>
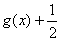 ;
;(Ⅲ)解:假设存在实数a,使f(x)=ax-ln(-x)有最小值3,x∈[-e,0),
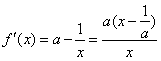 ,
,①当
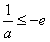 ,即
,即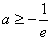 时,由于x∈[-e,0),则f′(x)=
时,由于x∈[-e,0),则f′(x)=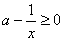 ,
,∴函数f(x)=ax-ln(-x)是[-e,0)上的增函数,
∴f(x)min=f(-e)=-ae-1=3,解得
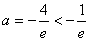 (舍去);
(舍去);②当
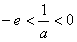 即
即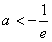 时,则当
时,则当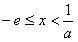 时,f′(x)=
时,f′(x)=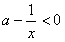 ,
,此时f(x)=ax-ln(-x)是减函数;
当
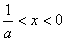 时,f′(x)=
时,f′(x)=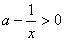 ,
,此时f(x)=ax-ln(-x)是增函数,
∴
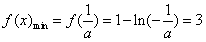 ,解得a=-e2,符合
,解得a=-e2,符合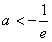 ;
; ③当
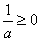 时,则f′(x)=
时,则f′(x)=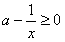 ,
, ∴函数f(x)=ax-ln(-x)是[-e,0)上的增函数,
∴f(x)min=f(-e)=-ae-1=3,解得
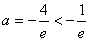 (舍去);
(舍去);综上所述存在实数a=-e2.

练习册系列答案
 学练快车道快乐假期寒假作业系列答案
学练快车道快乐假期寒假作业系列答案
相关题目