题目内容
已知函数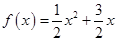 ,数列
,数列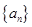 的前
的前 项和为
项和为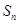 ,点
,点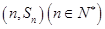 均在函数
均在函数 的图象上.
的图象上.
(1)求数列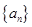 的通项公式
的通项公式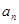 ;
;
(2)令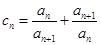 ,证明:
,证明: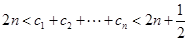 .
.
(1) ;(2)详见解析.
;(2)详见解析.
解析试题分析:(1)利用 时,
时, 以及
以及 时,
时, 以此求出数列
以此求出数列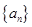 的通项公式;(2)利用基本不等式
的通项公式;(2)利用基本不等式 由此证明
由此证明 ,利用裂项法得到
,利用裂项法得到 ,由此计算出数列
,由此计算出数列 的前
的前 项和,于此证明
项和,于此证明 .
.
(1) 点
点 在
在 的图象上,
的图象上, ,
,
当 时,
时, ;
;
当 时,
时, 适合上式,
适合上式, ;
;
(2)证明:由 ,
, ,
,
又 ,
,
 ,
, 成立.
成立.
考点:1.定义法求数列通项;2.基本不等式;3.裂项法求和

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
设 是等差数列
是等差数列 的前
的前 项和,
项和,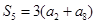 , 则
, 则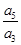 的值为( ).
的值为( ).
A. | B.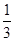 | C.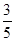 | D. |
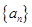 的通项为
的通项为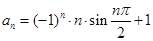 前
前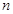 项和为
项和为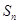 , 则
, 则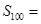 _________.
_________.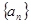 的前
的前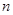 项和
项和 ,则
,则 ________________;
________________; 的前
的前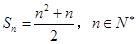 .
.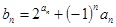 ,求数列
,求数列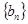 的前
的前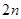 项和.
项和.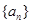 的前
的前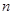 项和为
项和为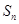 ,且
,且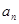 是
是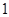 的等差中项,等差数列
的等差中项,等差数列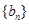 满足
满足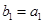 ,
,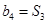 .
.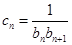 ,数列
,数列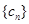 的前
的前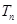 ,证明:
,证明: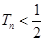 .
.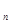 }满足0<a
}满足0<a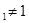 , 且
, 且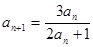 (n
(n N*).
N*). 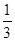 ,求出a2、a3、a4、a5的值,归纳出an , 并用数学归纳法证明.
,求出a2、a3、a4、a5的值,归纳出an , 并用数学归纳法证明.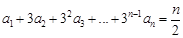 ,则
,则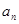 = .
= .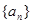 的前
的前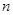 项和为
项和为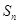 ,
,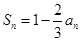 ,则
,则