题目内容
已知函数 是定义在
是定义在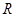 上的奇函数,且当
上的奇函数,且当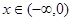 时,不等式
时,不等式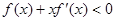 成立,若
成立,若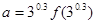 ,
,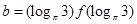 ,
,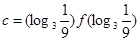 ,则
,则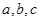 的大小关系是( )
的大小关系是( )
A.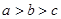 | B.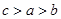 | C. | D.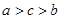 |
B
解析试题分析:因为 ,所以当
,所以当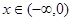 时,不等式
时,不等式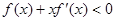 ,说明y=xf(x)在
,说明y=xf(x)在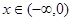 是减函数,又
是减函数,又 是定义在
是定义在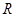 上的奇函数,所以y=xf(x)是偶函数,在(0,+
上的奇函数,所以y=xf(x)是偶函数,在(0,+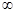 )是增函数。
)是增函数。
而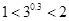 ,
,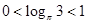 ,
,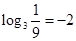 ,
,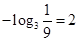 ,所以
,所以 ,有
,有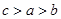 ,故选B。
,故选B。
考点:本题主要考查导数的运算法则,导数的应用,函数的奇偶性、单调性,指数函数、对数函数的性质。
点评:小综合题,利用导数的正负,可判断函数的单调性,利用奇偶性可知对称区间上函数单调性关系,综合应用数学知识的能力得到较好的考查。

练习册系列答案
相关题目
下列求导运算正确的是( )
A. | B. |
C. | D. |
函数 在闭区间
在闭区间 内的平均变化率为
内的平均变化率为
A. | B. | C. | D. |
已知函数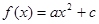 ,且
,且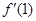 =2,则
=2,则 的值为
的值为
| A.1 | B.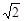 | C.-1 | D.0 |
已知函数 ,且
,且 ,
, 的导函数,函数
的导函数,函数 的图象如图所示.则平面区域
的图象如图所示.则平面区域 所围成的面积是( )
所围成的面积是( )
| A.2 | B.4 | C.5 | D.8 |
若曲线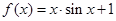 在
在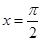 处的切线与直线ax+2y+1=0互相垂直,则实数a的值等于( )
处的切线与直线ax+2y+1=0互相垂直,则实数a的值等于( )
| A.-2 | B.-1 | C.1 | D.2 |
由曲线y=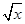 ,直线y=x-2及y轴所围成的图形的面积为
,直线y=x-2及y轴所围成的图形的面积为
A.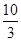 | B.4 | C.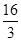 | D.6 |
曲线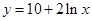 在点
在点 处的切线方程是
处的切线方程是
A. | B. |
C. | D.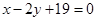 |
设定义在R上的函数 是最小正周期为
是最小正周期为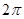 的偶函数,
的偶函数,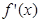 是
是 的导函数,当
的导函数,当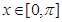 时,
时,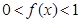 ;当
;当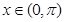 且
且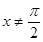 时,
时,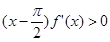 ,则函数
,则函数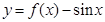 在
在 上的零点个数为
上的零点个数为
| A.2 | B.4 | C.5 | D.8 |