题目内容
若函数
的定义域是[n，n+1]（n为自然数） 那么f（x）的值域中的整数个数是 ．
【答案】分析：f（x）的对称轴是x=
，当n≥1时，f（x）在[n，n+1]上是单调递增的，因为f（n）和f（n+1）都不是整数，
故f（x）的值域中的整数个数问题只要计算f（n+1）-f（n）即可；n=0时，值域为[f（
），f（0）]．
解答：解：当n≥1时，f（x）在[n，n+1]上是单调递增的，
f（n+1）-f（n）=（n+1）2-（n+1）+
-n2+n-
=2n，故f（x）的值域中的整数个数是2n，
n=0时，值域为[f（
），f（0）]=[
，
]，无整数．
故答案为：2n
点评：本题考查二次函数的值域问题，对问题的化归转化能力．
，当n≥1时，f（x）在[n，n+1]上是单调递增的，因为f（n）和f（n+1）都不是整数，故f（x）的值域中的整数个数问题只要计算f（n+1）-f（n）即可；n=0时，值域为[f（
），f（0）]．解答：解：当n≥1时，f（x）在[n，n+1]上是单调递增的，
f（n+1）-f（n）=（n+1）2-（n+1）+
-n2+n-=2n，故f（x）的值域中的整数个数是2n，n=0时，值域为[f（
），f（0）]=[，]，无整数．故答案为：2n
点评：本题考查二次函数的值域问题，对问题的化归转化能力．
练习册系列答案
南大教辅抢先起跑暑假衔接教程南京大学出版社系列答案
相关题目
的定义域是{x|x＜1}，则a＜－1；
，则
(其中n∈N+)；
的定义域是[n，n+1]（n为自然数） 那么f（x）的值域中的整数个数是________．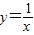
的定义域是{x|x＞2}，则它的值域是
；
．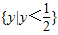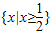