题目内容
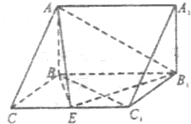 如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知AB=BC=1,BB1=2,
如图,在三棱柱ABC-A1B1C1中,AB⊥侧面BB1C1C,已知AB=BC=1,BB1=2,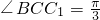 ,E为CC1的中点.
,E为CC1的中点.
(1)求证:C1B⊥平面ABC;
(2)求二面角A-B1E-B的大小.
(1)证明:因为AB⊥侧面BB1C1C,BCl?侧面BB1C1C,故AB⊥BCl,
在△BCCl中,BC=1,CC1=BB1=2,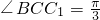 ,可得△BCE为等边三角形,BE=EC1,∠EBC1=
,可得△BCE为等边三角形,BE=EC1,∠EBC1= ,所以BC⊥BCl.
,所以BC⊥BCl.
而BC∩AB=B,∴C1B⊥平面ABC.(6分)
(2)解:在△B1C1E中,EC1=1,C1B1=1,∠B1C1E= ,
,
∴∠B1EC1=
∵∠BEC= ,∴BE⊥EBl.
,∴BE⊥EBl.
又∵AB⊥侧面BBlC1C,∴AB⊥BlE,
又AB∩BE=B,∴B1E⊥平面ABE,∴AE⊥BlE,
∴∠AEB即是二面角A-B1E-B的平面角.
在Rt△ABE中,tan∠AEB=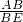 =1,故∠∠AEB=
=1,故∠∠AEB= .
.
所以二面角A-B1E-B的大小为 .(12分)
.(12分)
分析:(1)证明C1B⊥平面ABC,利用线面垂直的判定,证明AB⊥BCl,BC⊥BCl即可;
(2)证明∠AEB是二面角A-B1E-B的平面角,在Rt△ABE中,利用正切函数,即可求解.
点评:本题考查线面垂直,考查面面角,正确运用线面垂直的判定,作出面面角是关键.
在△BCCl中,BC=1,CC1=BB1=2,
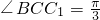 ,可得△BCE为等边三角形,BE=EC1,∠EBC1=
,可得△BCE为等边三角形,BE=EC1,∠EBC1= ,所以BC⊥BCl.
,所以BC⊥BCl.而BC∩AB=B,∴C1B⊥平面ABC.(6分)
(2)解:在△B1C1E中,EC1=1,C1B1=1,∠B1C1E=
 ,
,∴∠B1EC1=

∵∠BEC=
 ,∴BE⊥EBl.
,∴BE⊥EBl.又∵AB⊥侧面BBlC1C,∴AB⊥BlE,
又AB∩BE=B,∴B1E⊥平面ABE,∴AE⊥BlE,
∴∠AEB即是二面角A-B1E-B的平面角.
在Rt△ABE中,tan∠AEB=
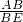 =1,故∠∠AEB=
=1,故∠∠AEB= .
.所以二面角A-B1E-B的大小为
 .(12分)
.(12分)分析:(1)证明C1B⊥平面ABC,利用线面垂直的判定,证明AB⊥BCl,BC⊥BCl即可;
(2)证明∠AEB是二面角A-B1E-B的平面角,在Rt△ABE中,利用正切函数,即可求解.
点评:本题考查线面垂直,考查面面角,正确运用线面垂直的判定,作出面面角是关键.

练习册系列答案
相关题目
 如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )
如图,在三棱柱ABC-A'B'C'中,若E、F分别为AB、AC的中点,平面EB'C'F将三棱柱分成体积为V1、V2的两部分,那么V1:V2为( )| A、3:2 | B、7:5 | C、8:5 | D、9:5 |
 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,A1A=AC=2,BC=1,AB=
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,A1A=AC=2,BC=1,AB= 如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3
如图,在三棱柱ABC-A1B1C1中,四边形A1ABB1为菱形,∠A1AB=60°,四边形BCC1B1为矩形,若AB⊥BC且AB=4,BC=3 (2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2
(2013•通州区一模)如图,在三棱柱ABC-A1B1C1中,CC1⊥底面ABC,AC=BC=2,AB=2 如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.
如图,在三棱柱ABC-A1B1C1中,AA1⊥面ABC,AC⊥BC,E分别在线段B1C1上,B1E=3EC1,AC=BC=CC1=4.