题目内容
对于数列{an}，定义数列{an+1-an}为数列{an}的“差数列”，若a1=2，{an}的“差数列”的通项为2n，则数列{an}的通项公式an=________．
2n
分析：先根据an+1-an=2n，对数列进行叠加，最后求得an=2n．
解答：∵an+1-an=2n，
∴an=（an-an-1）+（an-1-an-2）+…+（a2-a1）+a1
=2n-1+2n-2++22+2+2=2+（2+22+23+…+2n-1）=2+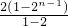
=2n，
故答案为 2n．
点评：本题主要考查数列的递推式，对于an+1-an=p的形式常可用叠加法求得数列通项公式，属于中档题．
分析：先根据an+1-an=2n，对数列进行叠加，最后求得an=2n．
解答：∵an+1-an=2n，
∴an=（an-an-1）+（an-1-an-2）+…+（a2-a1）+a1
=2n-1+2n-2++22+2+2=2+（2+22+23+…+2n-1）=2+
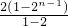=2n，故答案为 2n．
点评：本题主要考查数列的递推式，对于an+1-an=p的形式常可用叠加法求得数列通项公式，属于中档题．
练习册系列答案
导学全程练创优训练系列答案
相关题目
，数列{an}满足an+1=H（an）（n∈N*），且a1∈（0，1），试判断an+1与an的大小，并证明之．
，数列{an}满足an+1=H（an）（n∈N*），且a1∈（0，1），试判断an+1与an的大小，并证明之．