题目内容
如图,在底面是正方形的四棱锥 中,
中, ,
, ,点
,点 在
在 上,且
上,且 .
.
(Ⅰ)求证: 平面
平面 ;
;
(Ⅱ)求二面角 的余弦值;
的余弦值;
(Ⅲ)在棱 上是否存在一点
上是否存在一点 ,使得
,使得 平面
平面 .
.
解:(Ⅰ)正方形 边长为1,
边长为1, ,
, ,
,
所以 ,即
,即 ,
, ,
,
因为 ,
,
所以 平面
平面 .
.
(Ⅱ)如图,以 为坐标原点,直线
为坐标原点,直线 ,
, ,
, 分别为
分别为 轴,
轴, 轴,
轴, 轴,建立空间直角坐标系,则
轴,建立空间直角坐标系,则 ,
, .
.
 由(Ⅰ)知
由(Ⅰ)知 为平面
为平面 的法向量,
的法向量,
 ,
,
设平面 的法向量为
的法向量为 ,
,
由 ,
, ,
,
得
令 ,则
,则 ,
, ,
,
所以 ,
,
所以 ,
,
即所求二面角的余弦值为 .
.
(Ⅲ)设 ,则
,则 ,
,
 ,
,
若 平面
平面 ,则
,则 ,即
,即 ,
, ,
,
解得 ,
,
所以存在满足题意的点,
当 是棱
是棱 的中点时,
的中点时, 平面
平面 . …………12分
. …………12分

练习册系列答案
相关题目
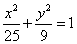 的两个焦点分别为F1、F2,P为椭圆上的一点,已知PF1
的两个焦点分别为F1、F2,P为椭圆上的一点,已知PF1 PF2,则
PF2,则 PF1F2的面积为 ( )
PF1F2的面积为 ( ) 中的
中的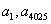 是函数
是函数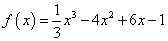 的极值点,则
的极值点,则 等于
等于 (x≠0) (B)
(x≠0) (B) (x≠0)
(x≠0)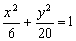 (x≠0) (D)
(x≠0) (D)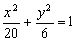 (x≠0)
(x≠0) 的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率
的左、右焦点,过F1且垂直于x轴的直线与椭圆交于A、B两点,若△ABF2为正三角形,则该椭圆的离心率 为 ( )
为 ( ) (B)
(B)  (C)
(C) (D)
(D)
 ,
, ,
, 的图象上的任意一点
的图象上的任意一点 满足条件
满足条件 ,则称函数
,则称函数 具有性质
具有性质 ,那么下列函数值具有性质
,那么下列函数值具有性质 B.
B. C.
C. D.
D.