题目内容
定义在R上的函数y=f(x)满足f(4-x)=f(x),(x-2)·f′(x)<0,若x1<x2且x1+x2>4,则 ( ).
A.f(x1)<f(x2)
B.f(x1)>f(x2)
C.f(x1)=f(x2)
D.f(x1)与f(x2)的大小不确定
解析 ∵f(4-x)=f(x),∴函数f(x)的图象关于直线x=2对称,由(x-2)f′(x)<0可得函数f(x)在(-∞,2)上单调递增,在(2,+∞)上单调递减,∴当x2>x1>2时,f(x1)>f(x2);当x2>2>x1时,∵x1+x2>4,∴x2>4-x1>2,∴f(4-x1)=f(x1)>f(x2),综上,f(x1)>f(x2),故选B.
答案 B

练习册系列答案
相关题目
 的值是
( )
的值是
( )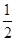 B.2 C.3 D.0
B.2 C.3 D.0