题目内容
已知函数f(x)=kx2+(k-1)x(k为常数)
(1)若k=2,解不等式f(x)>0;
(2)若k>0,解不等式f(x)>0;
(3)若k>0,且对于任意x∈[1,+∞),总有g(x)=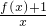 ≥1成立,求k的取值范围.
≥1成立,求k的取值范围.
解:(1)若k=2,则不等式f(x)>0可化为2x2+x>0,
解之,得{x|x>0,或x<- }.
}.
(2)若k>0,则不等式f(x)>0可转化为kx•(x-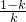 )>0,
)>0,
当0<k<1时,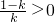 ,此时x>
,此时x>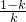 或x<0,
或x<0,
当k>1时,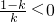 ,此时
,此时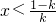 ,或x>0.
,或x>0.
当k=0时,f(x)=x2>0,此时x≠0,
综上所述:当0<k<1时,x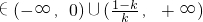 ,
,
当k>1时,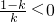 ,此时,
,此时,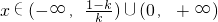 ,
,
当k=1时,f(x)=x2>0,
此时,x∈(-∞,0)∪(0,+∞).
(3)因为k>0,x>0,
所以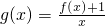 =kx+
=kx+ +k-1≥
+k-1≥ +k-1=2
+k-1=2 +k-1,
+k-1,
当且仅当kx= (x>0),即x=
(x>0),即x=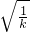 时取等号,
时取等号,
又x∈[1,+∞),所以当0<k≤1时,x=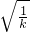 ∈[1,+∞),上述等到可以取到.
∈[1,+∞),上述等到可以取到.
此时,由2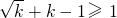 ,得k
,得k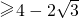 ,
,
∵0<k≤1,故k∈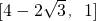 ;
;
当k>1,x=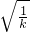 ∈[1,+∞),上述等号取不到,
∈[1,+∞),上述等号取不到,
此时g(x)=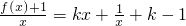 在[1,+∞)上是增函数,
在[1,+∞)上是增函数,
故g(x)min=g(1)=2k,
由2k≥1,得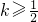 ,∵k>1,∴k∈[1,+∞),
,∵k>1,∴k∈[1,+∞),
综上可知 ∪[1,+∞)=[4-2
∪[1,+∞)=[4-2 ,+∞).
,+∞).
分析:(1)若k=2,则不等式f(x)>0可化为2x2+x>0,由此能够求出不等式f(x)>0的解.
(2)若k>0,则不等式f(x)>0可转化为kx•(x-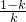 )>0,分0<k<1,k>1,k=0三种情况,能够求出不等式f(x)>0的解.
)>0,分0<k<1,k>1,k=0三种情况,能够求出不等式f(x)>0的解.
(3)因为k>0,x>0,所以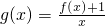 =kx+
=kx+ +k-1≥
+k-1≥ +k-1=2
+k-1=2 +k-1,当且仅当kx=
+k-1,当且仅当kx= (x>0),即x=
(x>0),即x=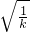 时取等号,由此入手能够求出k的取值范围.
时取等号,由此入手能够求出k的取值范围.
点评:本题考查函数的恒成立问题的灵活运用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.
解之,得{x|x>0,或x<-
 }.
}.(2)若k>0,则不等式f(x)>0可转化为kx•(x-
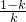 )>0,
)>0,当0<k<1时,
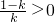 ,此时x>
,此时x>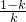 或x<0,
或x<0,当k>1时,
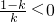 ,此时
,此时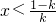 ,或x>0.
,或x>0.当k=0时,f(x)=x2>0,此时x≠0,
综上所述:当0<k<1时,x
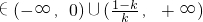 ,
,当k>1时,
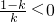 ,此时,
,此时,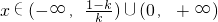 ,
,当k=1时,f(x)=x2>0,
此时,x∈(-∞,0)∪(0,+∞).
(3)因为k>0,x>0,
所以
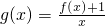 =kx+
=kx+ +k-1≥
+k-1≥ +k-1=2
+k-1=2 +k-1,
+k-1,当且仅当kx=
 (x>0),即x=
(x>0),即x=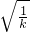 时取等号,
时取等号,又x∈[1,+∞),所以当0<k≤1时,x=
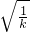 ∈[1,+∞),上述等到可以取到.
∈[1,+∞),上述等到可以取到.此时,由2
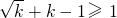 ,得k
,得k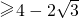 ,
,∵0<k≤1,故k∈
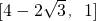 ;
;当k>1,x=
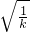 ∈[1,+∞),上述等号取不到,
∈[1,+∞),上述等号取不到,此时g(x)=
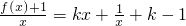 在[1,+∞)上是增函数,
在[1,+∞)上是增函数,故g(x)min=g(1)=2k,
由2k≥1,得
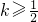 ,∵k>1,∴k∈[1,+∞),
,∵k>1,∴k∈[1,+∞),综上可知
 ∪[1,+∞)=[4-2
∪[1,+∞)=[4-2 ,+∞).
,+∞).分析:(1)若k=2,则不等式f(x)>0可化为2x2+x>0,由此能够求出不等式f(x)>0的解.
(2)若k>0,则不等式f(x)>0可转化为kx•(x-
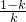 )>0,分0<k<1,k>1,k=0三种情况,能够求出不等式f(x)>0的解.
)>0,分0<k<1,k>1,k=0三种情况,能够求出不等式f(x)>0的解.(3)因为k>0,x>0,所以
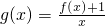 =kx+
=kx+ +k-1≥
+k-1≥ +k-1=2
+k-1=2 +k-1,当且仅当kx=
+k-1,当且仅当kx= (x>0),即x=
(x>0),即x=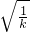 时取等号,由此入手能够求出k的取值范围.
时取等号,由此入手能够求出k的取值范围.点评:本题考查函数的恒成立问题的灵活运用,考查运算求解能力,推理论证能力;考查函数与方程思想,化归与转化思想.综合性强,难度大,有一定的探索性,对数学思维能力要求较高,是高考的重点.解题时要认真审题,仔细解答.

练习册系列答案
相关题目