Question

已知函数f(x)＝sin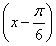＋cos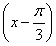，g(x)＝2sin2.

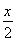(1)若α是第一象限角，且f(α)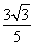＝，求g(α)的值；

(2)求使f(x)≥g(x)成立的x的取值集合．

 

Answer 1

（1）（2）

【解析】f(x)＝sin＋cos＝sinx－cosx＋cosx＋sinx＝sinx，

g(x)＝2sin2＝1－cos x.

(1)由f(α)＝得sin α＝.又α是第一象限角，所以cos α＞0.

从而g(α)＝1－cos α＝1－＝1－＝.

(2)f(x)≥g(x)等价于sin x≥1－cos x，即sin x＋cos x≥1，于是sin≥，

从而2kπ＋≤x＋≤2kπ＋，k∈Z，即2kπ≤x≤2kπ＋，k∈Z，

故使f(x)≥g(x)成立的x的取值集合为