题目内容
如图,已知椭圆C:![]() (a>0,b>0)过点P(
(a>0,b>0)过点P(![]() ),上、下焦点分别为F1、F2,向量
),上、下焦点分别为F1、F2,向量![]() .直线l与椭圆交于A,B两点,线段AB中点为m(
.直线l与椭圆交于A,B两点,线段AB中点为m(![]() ).
).
(1)求椭圆C的方程;
(2)求直线l的方程;
(3)记椭圆在直线l下方的部分与线段AB所围成的平面区域(含边界)为D,若曲线x2﹣2mx+y2+4y+m2﹣4=0与区域D有公共点,试求m的最小值.
考点:
直线与圆锥曲线的综合问题;平面向量数量积的运算;椭圆的标准方程.
分析:
(1)把点B代入椭圆的方程,利用向量垂直,及几何量之间的关系,联立方程求得a和b,则椭圆的方程可得;
(2)分类讨论,利用线段AB中点坐标,结合韦达定理,可求直线的方程;
(3)把圆的方程整理成标准方程求得圆心和半径,进而利用图象可知只须考虑m<0的情形.设出圆与直线的切点,利用点到直线的距离求得m,进而可求得过点G与直线l垂直的直线的方程,把两直线方程联立求得T,因为区域D内的点的横坐标的最小值与最大值分别为﹣1,2,所以切点T∉D,由图可知当⊙G过点B时,m取得最小值,利用两点间的距离公式求得m的最小值.
解答:
解:(1)∵椭圆C:![]() (a>0,b>0)过点P(
(a>0,b>0)过点P(![]() ),∴
),∴![]()
∵向量![]() ,∴4c2=2+(
,∴4c2=2+(![]() ﹣c)2+2+(
﹣c)2+2+(![]() ﹣c)2,∴c=2
﹣c)2,∴c=2![]()
又a2=b2+c2,∴a2=12,b2=4
∴椭圆方程为![]()
(2)①当斜率k不存在时,由于点M不是线段AB的中点,所以不符合要求;
②当斜率k存在时,设直线l方程为y+![]() =k(x﹣
=k(x﹣![]() ),代入椭圆方程整理得
),代入椭圆方程整理得
(3+k2)x2﹣(k2+3k)x+![]() k2﹣
k2﹣![]() =0
=0
∵线段AB中点为m(![]() ),∴
),∴![]() =
=![]()
∴k=1
∴直线l:x﹣y﹣2=0
(3)化简曲线方程得:(x﹣m)2+(y+2)2=8,是以(m,﹣2)为圆心,2![]() 为半径的圆.
为半径的圆.
表示圆心在直线y=﹣2上,半径为2![]() 的动圆.
的动圆.
由于要求实数m的最小值,由图可知,只须考虑m<0的情形.
当圆与直线相切时,![]() ,此时为m=﹣4,圆心(﹣4,﹣2).
,此时为m=﹣4,圆心(﹣4,﹣2).
当m=﹣4时,过点G(﹣4,﹣2)与直线l垂直的直线l'的方程为x+y+6=0,
解方程组![]() ,得T(﹣2,﹣4).
,得T(﹣2,﹣4).
因为区域D内的点的横坐标的最小值与最大值分别为﹣1,2,
所以切点T∉D,由图可知当⊙G过点B时,m取得最小值,即(﹣1﹣m)2+(﹣3+2)2=8,解得mmin=﹣![]() ﹣1.
﹣1.

点评:
本题考查椭圆与直线的方程,考查直线与圆锥曲线的综合问题,同时考查了知识的综合运用和数形结合的方法的应用.

 如图,已知椭圆C:
如图,已知椭圆C: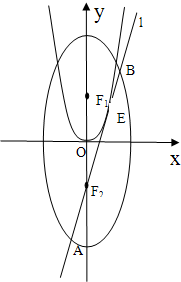 如图,已知椭圆
如图,已知椭圆 如图,已知椭圆C:
如图,已知椭圆C: 如图,已知椭圆
如图,已知椭圆 (2012•梅州一模)如图,已知椭圆C:
(2012•梅州一模)如图,已知椭圆C: