题目内容
已知数列![]() 的前
的前![]() 项和
项和![]() 满足:
满足:![]() ,
, ![]()
(1)写出数列![]() 的前三项
的前三项![]() ,
,![]() ,
,![]() ;
;
(2)求数列![]() 的通项公式;
的通项公式;
(3)证明:对任意的整数![]() ,有
,有![]()
证明见解析
解析:
⑴由递推公式易求:a1=1,a2=0,a3=2;
⑵由已知得:![]() (n>1)
(n>1)
化简得:![]()
![]() ,
,![]()
故数列{![]() }是以
}是以![]() 为首项, 公比为
为首项, 公比为![]() 的等比数列.
的等比数列.
故![]() ∴
∴![]()
∴数列{![]() }的通项公式为:
}的通项公式为:![]() .
.
⑶观察要证的不等式,左边很复杂,先要设法对左边的项进行适当的放缩,使之能够求和。而左边=![]() ,如果我们把上式中的分母中的
,如果我们把上式中的分母中的![]() 去掉,就可利用等比数列的前n项公式求和,由于-1与1交错出现,容易想到将式中两项两项地合并起来一起进行放缩,尝试知:
去掉,就可利用等比数列的前n项公式求和,由于-1与1交错出现,容易想到将式中两项两项地合并起来一起进行放缩,尝试知:![]() ,
,
![]() ,因此,可将
,因此,可将![]() 保留,再将后面的项两两组合后放缩,即可求和。这里需要对
保留,再将后面的项两两组合后放缩,即可求和。这里需要对![]() 进行分类讨论,(1)当
进行分类讨论,(1)当![]() 为偶数
为偶数![]() 时,
时,
![]()
![]()
![]()
![]()
![]()
![]()
(2)当![]() 是奇数
是奇数![]() 时,
时,![]() 为偶数,
为偶数,
![]()
所以对任意整数![]() ,有
,有![]()
![]() 。
。

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
 的前
的前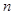 项和
项和 满足:
满足: ,且
,且 ,那么
,那么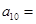 ( )
( ) 的前
的前 项和
项和 满足
满足 ,等差数列
,等差数列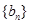 满足
满足 ,
, 。
。 ,数列
,数列 的前
的前 ,问
,问 >
> 的最小正整数
的最小正整数