Question

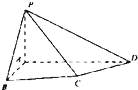如图，四棱锥P-ABCD中，PA⊥底面ABCD，四边形ABCD中，AB⊥AD，AB+AD=4，CD=

2

，∠CDA=45°．
（1）求证：平面PAB⊥平面PAD；
（2）设AB=AP．若直线PB与平面PCD所成的角为30°，求线段AB的长．

Answer 1

分析：（1）证明平面PAB⊥平面PAD，只需证明AB⊥平面PAD，只需证明PA⊥AB，AB⊥AD；
（2）以A为坐标原点，建立空间直角坐标系，在平面ABCD内，作CE∥AB交AD于点E，求出平面PCD的一个法向量，利用直线PB与平面PCD所成的角为30°，建立方程，即可求线段AB的长．

解答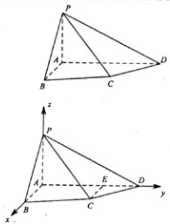：（1）证明：因为PA⊥平面ABCD，AC?平面ABCD，
所以PA⊥AB，
又AB⊥AD，PA∩AD=A，
所以AB⊥平面PAD．
又AB?平面PAB，所以平面PAB⊥平面PAD．（6分）
（2）解：以A为坐标原点，建立空间直角坐标系A-xyz（如图）
在平面ABCD内，作CE∥AB交AD于点E，则CE⊥AD．
在Rt△CDE中，DE=CD•cos45°=1，CE=CD•sin45°=1，
设AB=AP=t，则B（t，0，0），P（0，0，t）
由AB+AD=4，得AD=4-t，
所以E（0，3-t，0），C（1，3-t，0），D（0，4-t，0），

CD

=(-1，1，0)，

PD

=(0，4-t，-t)．
设平面PCD的法向量为

n

=（x，y，z），
由

n

⊥

CD

，

n

⊥

PD

，得

-x+y=0 (4-t)y-tx=0.

取x=t，得平面PCD的一个法向量

n

=（t，t，4-t），
又

PB

=(t，0，-t)，故由直线PB与平面PCD所成的角为30°，得cos60°=|

n • PB

| n || PB |

|，即

|2t2-4t|

t2+t2+(4-t)2 • 2x2

=

1

2

，
解得t=

4

5

或t=4（舍去，因为AD=4-t＞0），所以AB=

4

5

．（14分）

点评：本题考查线面垂直，考查面面垂直，考查线面角，考查向量知识的运用，正确求平面的法向量，向量的夹角公式是关键．