题目内容
(本小题满分14分)如图,已知直线OP1,OP2为双曲线E: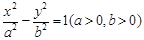 的渐近线,△P1OP2的面积为
的渐近线,△P1OP2的面积为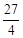 ,在双曲线E上存在点P为线段P1P2的一个三等分点,且双曲线E的离心率为
,在双曲线E上存在点P为线段P1P2的一个三等分点,且双曲线E的离心率为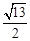 .
.
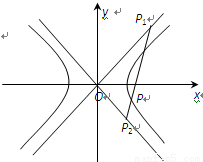
(1)若P1、P2点的横坐标分别为x1、x2,则x1、x2之间满足怎样的关系?并证明你的结论;
(2)求双曲线E的方程;
(3)设双曲线E上的动点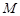 ,两焦点
,两焦点 ,若
,若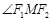 为钝角,求
为钝角,求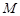 点横坐标
点横坐标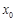 的取值范围.
的取值范围.
(1)∴x1·x2=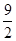 ;(2)
;(2)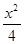 -
-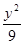 =1;(3)-
=1;(3)-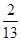
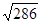 ,-2)∪(2,
,-2)∪(2,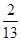
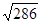 )
)
【解析】
试题分析:(1)设双曲线方程为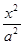 -
-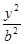 =1,由已知得
=1,由已知得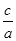 =
=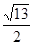
∴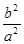 =
=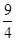 ∴渐近线方程为y=±
∴渐近线方程为y=±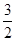 x …………2分
x …………2分
则P1(x1,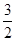 x1) P2(x2,-
x1) P2(x2,-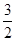 x2)
x2)
设渐近线y=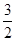 x的倾斜角为θ,则tanθ=
x的倾斜角为θ,则tanθ=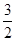 ∴sin2θ=
∴sin2θ=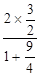 =
=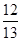
∴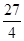 =
=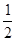 |OP1||OP2|sin2θ=
|OP1||OP2|sin2θ=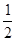
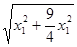
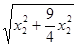 ·
·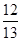
∴x1·x2=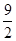 …………5分
…………5分
(2)不妨设P分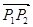 所成的比为λ=2,P(x,y), 则
所成的比为λ=2,P(x,y), 则
x=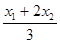 y=
y=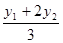 =
=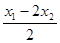
∴x1+2x2=3x x1-2x2=2y …………7分
∴(3x)2-(2y)2=8x1x2=36
∴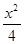 -
-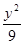 =1 即为双曲线E的方程 …………9分
=1 即为双曲线E的方程 …………9分
(3)由(2)知C=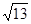 ,∴F1(-
,∴F1(-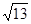 ,0) F2(
,0) F2(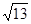 ,0) 设M(x0,y0)
,0) 设M(x0,y0)
则y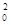 =
=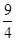 x
x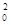 -9,
-9,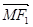 =(-
=(-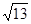 -x0,-y0)
-x0,-y0) 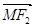 =(
=(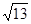 -x0,-y0)
-x0,-y0)
∴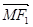 ·
·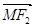 =x
=x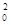 -13+y
-13+y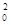 =
=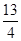 x
x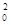 -22 …………12分
-22 …………12分
若∠F1MF2为钝角,则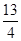 x
x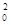 -22<0
-22<0
∴|x0|<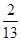
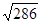 又|x0|>2
又|x0|>2
∴x0的范围为(-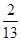
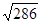 ,-2)∪(2,
,-2)∪(2,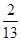
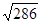 ) ……14分
) ……14分
考点:本题考查了双曲线的方程、性质及数量积的运用
点评:本题主要考查双曲线的标准方程和性质、数量积的应用等基础知识,考查曲线和方程的关系等解析几何的基本思想方法

 =2,点(
=2,点( )在函数
)在函数 的图像上,其中
的图像上,其中 =
= .
. }是等比数列;
}是等比数列; ,求
,求 及数列{
及数列{ }的通项公式;
}的通项公式; ,求数列{
,求数列{ }的前n项和
}的前n项和 ,并证明
,并证明 .
. 天(
天( )的销售价格(单位:元)为
)的销售价格(单位:元)为 ,第
,第 ,已知该商品成本为每件25元.
,已知该商品成本为每件25元. 关于第
关于第 的图像在点
的图像在点 处的切线与直线
处的切线与直线 平行.
平行. ,
, 满足的关系式;
满足的关系式; 上恒成立,求
上恒成立,求 (
( )
)