题目内容
数列{an}的前n项和为Sn,a1=1,an+1=2Sn(n∈N+).(Ⅰ)证明数列{Sn}是等比数列;
(Ⅱ)求数列{an}的通项an;
(Ⅲ)求数列{n•an}的前n项和Tn.
【答案】分析:(Ⅰ)要证一个数列为等比数列,就是要证明这个数列的每一项与它的前一项的之比是一个常数.
(Ⅱ)由(Ⅰ)知Sn=3n-1(n∈N*),又an+1=2Sn(n∈N+)可求n≥2时an通项,知a1=1,所以可求n∈N*时an通项.
(Ⅲ)在Tn 的等式两边同乘以3得到一个新的等式,两式左右两边分别相减,再用等比数列的前n项和可求Tn
解答:解:(Ⅰ)∵an+1=2Sn,∴Sn+1-Sn=2Sn,∴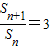 .
.
又∵S1=a1=1,
∴数列{Sn}是首项为1,公比为3的等比数列,Sn=3n-1(n∈N*).…(4分)
(Ⅱ)当n≥2时,an=2Sn-1=2•3n-2(n≥2),
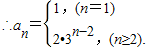 …(8分)
…(8分)
(Ⅲ) Tn=a1+2a2+3a3+…+nan,
当n=1时,T1=1;
当n≥2时,Tn=1+4•3+6•31+…+2n•3n-2,…①
3Tn=3+4•31+6•32+…+2n•3n-1,…②…(11分)
①-②得:-2Tn=-2+4+2(31+32+…+3n-2)-2n•3n-1
=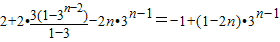
∴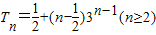 . …(13分)
. …(13分)
又∵T1=a1=1也满足上式,
∴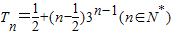 . …(14分)
. …(14分)
点评:求通项公式时,注意验证n=1;用错位相减法求数列的前n项和,要观察项的特征,是否是等差数列的项与等比数列的项的乘积.
(Ⅱ)由(Ⅰ)知Sn=3n-1(n∈N*),又an+1=2Sn(n∈N+)可求n≥2时an通项,知a1=1,所以可求n∈N*时an通项.
(Ⅲ)在Tn 的等式两边同乘以3得到一个新的等式,两式左右两边分别相减,再用等比数列的前n项和可求Tn
解答:解:(Ⅰ)∵an+1=2Sn,∴Sn+1-Sn=2Sn,∴
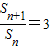 .
.又∵S1=a1=1,
∴数列{Sn}是首项为1,公比为3的等比数列,Sn=3n-1(n∈N*).…(4分)
(Ⅱ)当n≥2时,an=2Sn-1=2•3n-2(n≥2),
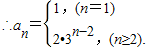 …(8分)
…(8分)(Ⅲ) Tn=a1+2a2+3a3+…+nan,
当n=1时,T1=1;
当n≥2时,Tn=1+4•3+6•31+…+2n•3n-2,…①
3Tn=3+4•31+6•32+…+2n•3n-1,…②…(11分)
①-②得:-2Tn=-2+4+2(31+32+…+3n-2)-2n•3n-1
=
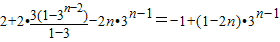
∴
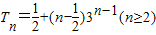 . …(13分)
. …(13分)又∵T1=a1=1也满足上式,
∴
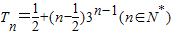 . …(14分)
. …(14分)点评:求通项公式时,注意验证n=1;用错位相减法求数列的前n项和,要观察项的特征,是否是等差数列的项与等比数列的项的乘积.

练习册系列答案
 综合自测系列答案
综合自测系列答案
相关题目