题目内容
已知函数 。
。
(Ⅰ)讨论f(x)的奇偶性;
(Ⅱ)判断f(x)在(-∞,0)上的单调性并用定义证明。
 。
。(Ⅰ)讨论f(x)的奇偶性;
(Ⅱ)判断f(x)在(-∞,0)上的单调性并用定义证明。
解:(Ⅰ) ,
, ,
,
令f(x)= f(-x),则 ,无解,∴f(x)不是偶函数;
,无解,∴f(x)不是偶函数;
令f(-x)=-f(x),则a=0,显然a=0时,f(x)为奇函数;
综上,当a=0时,f(x)为奇函数;当a≠0时,f(x)不具备奇偶性。
(Ⅱ)函数f(x)在(-∞,0)上单调递增,
证明:任取 ,且
,且 ,则
,则

 ,
,
∵ ,且
,且 ,
,
∴ ,
, ,
,
从而 ,故
,故 ,
,
∴f(x)在(-∞,0)上单调递增。
 ,
, ,
,令f(x)= f(-x),则
 ,无解,∴f(x)不是偶函数;
,无解,∴f(x)不是偶函数;令f(-x)=-f(x),则a=0,显然a=0时,f(x)为奇函数;
综上,当a=0时,f(x)为奇函数;当a≠0时,f(x)不具备奇偶性。
(Ⅱ)函数f(x)在(-∞,0)上单调递增,
证明:任取
 ,且
,且 ,则
,则 
 ,
,∵
 ,且
,且 ,
,∴
 ,
, ,
,从而
 ,故
,故 ,
,∴f(x)在(-∞,0)上单调递增。

练习册系列答案
相关题目
 ,其中
,其中 .(1) 讨论函数
.(1) 讨论函数 的单调性,并求出
的单调性,并求出 ,都存在
,都存在 ,使得
,使得 ,求实数
,求实数 的取值范围.
的取值范围. .
. 的单调性;
的单调性; ,证明:当
,证明:当 时,
时, ;
; 的图像与x轴交于A,B两点,线段AB中点的横坐标为x0,
的图像与x轴交于A,B两点,线段AB中点的横坐标为x0, (x0)<0.
(x0)<0. .
. 函数
函数 的单调性;
的单调性; 为偶数时,正项数列
为偶数时,正项数列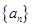 满足
满足 ,求
,求 时,求证:
时,求证: .
.