题目内容
已知函数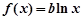 ,
,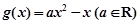
(1)若曲线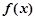 与
与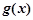 在公共点
在公共点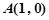 处有相同的切线,求实数
处有相同的切线,求实数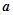 、
、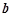 的值;
的值;
(2)当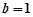 时,若曲线
时,若曲线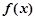 与
与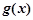 在公共点
在公共点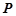 处有相同的切线,求证:点
处有相同的切线,求证:点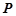 唯一;
唯一;
(3)若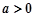 ,
,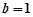 ,且曲线
,且曲线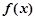 与
与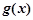 总存在公切线,求正实数
总存在公切线,求正实数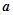 的最小值
的最小值
(1)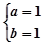 ;(2)详见解析;(3)正实数
;(2)详见解析;(3)正实数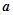 的最小值为1
的最小值为1
解析试题分析:(1)求实数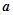 、
、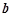 的值,因为曲线
的值,因为曲线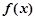 与
与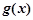 在公共点
在公共点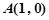 处有相同的切线,由导数的几何意义可得,
处有相同的切线,由导数的几何意义可得,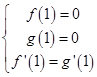 ,解出即可;(2)当
,解出即可;(2)当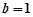 时,若曲线
时,若曲线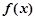 与
与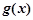 在公共点
在公共点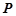 处有相同的切线,求证:点
处有相同的切线,求证:点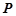 唯一,可设
唯一,可设 ,由题设得
,由题设得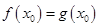 ,
, ,转化为关于
,转化为关于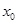 的方程
的方程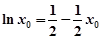 只有一解,进而构造函数,转化为函数只有一个零点,可利用导数即可证明;(3)设曲线
只有一解,进而构造函数,转化为函数只有一个零点,可利用导数即可证明;(3)设曲线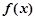 在点
在点 处的切线方程为
处的切线方程为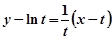 ,则只需使该切线
,则只需使该切线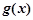 相切即可,也即方程组
相切即可,也即方程组 只有一解即可,所以消
只有一解即可,所以消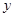 后
后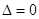 ,问题转化关于
,问题转化关于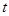 的方程总有解,分情况借助导数进行讨论即可求得
的方程总有解,分情况借助导数进行讨论即可求得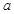 值最小值
值最小值
试题解析:(1)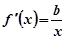 ,
,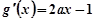 ∵曲线
∵曲线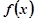 与
与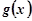 在公共点
在公共点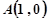 处有相同的切线∴
处有相同的切线∴ 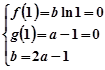 , 解得,
, 解得,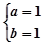 3分
3分
(2)设 ,则由题设有
,则由题设有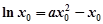 ①又在点
①又在点 有共同的切线
有共同的切线
∴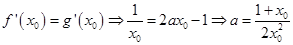 代入①得
代入①得 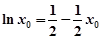 5分
5分
设 ,则
,则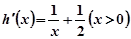 ,
,
∴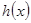 在
在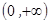 上单调递增,所以
上单调递增,所以 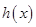 =0最多只有
=0最多只有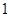 个实根,
个实根,
从而,结合(1)可知,满足题设的点 只能是
只能是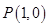 7分
7分
(3)当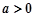 ,
,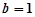 时,
时,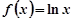 ,
,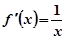 ,
,
曲线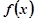 在点
在点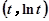 处的切线方程为
处的切线方程为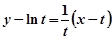 ,即
,即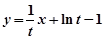
由 ,得
,得 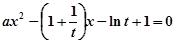
∵ 曲线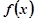 与
与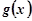 总存在公切线,∴ 关于
总存在公切线,∴ 关于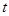
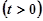 的方程
的方程 ,
,
即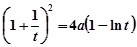
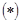 总有解 9分
总有解 9分
若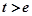 ,则
,则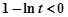 ,而
,而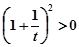 ,显然
,显然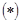 不成立,所以
不成立,所以 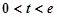 10分
10分
从而,方程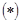 可化为
可化为 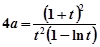
令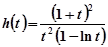
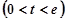 ,则
,则
练习册系列答案
 导学全程练创优训练系列答案
导学全程练创优训练系列答案
相关题目
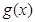 及二次函数
及二次函数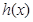 满足:
满足: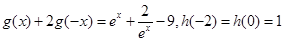 且
且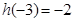 。
。 ;
;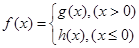 ,讨论方程
,讨论方程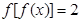 的解的个数情况.
的解的个数情况.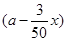 (a>0)万元.
(a>0)万元.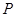 和
和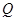 (万元),它们与投入资金
(万元),它们与投入资金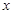 (万元)的关系依次是:其中
(万元)的关系依次是:其中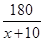 ,B产品的利润y2与投资金额x的函数关系为y2=
,B产品的利润y2与投资金额x的函数关系为y2=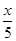 (注:利润与投资金额单位:万元).
(注:利润与投资金额单位:万元).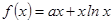 的图象在点
的图象在点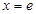 (e为自然对数的底数)处取得极值-1.
(e为自然对数的底数)处取得极值-1.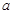 的值;
的值; 对任意
对任意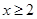 恒成立,求
恒成立,求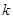 的取值范围.
的取值范围.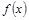 与第x天近似地满足
与第x天近似地满足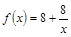 (千人),且参观民俗文化村的游客人均消费
(千人),且参观民俗文化村的游客人均消费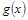 近似地满足
近似地满足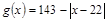 (元).
(元).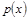 (单位千元,1≤x≤30,
(单位千元,1≤x≤30,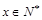 )的函数关系;
)的函数关系;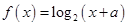 .
.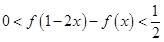 ,当
,当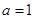 时,求
时,求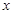 的取值范围;
的取值范围; 上奇函数
上奇函数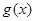 满足
满足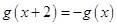 ,且当
,且当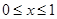 时,
时,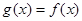 ,求
,求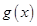 在
在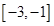 上的反函数
上的反函数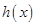 ;
;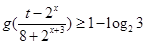 在
在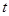 的取值范围.
的取值范围.