题目内容
已知实数x、y满足x2+y2-4y+1=0.(1)求![]() 的取值范围;
的取值范围;
(2)求y-2x的取值范围.
解析:(1)令k=![]() ,则直线y=kx与圆x2+(y-2)2=3有公共点,
,则直线y=kx与圆x2+(y-2)2=3有公共点,
∴直线与圆相交或相切.故圆心(0,2)到直线kx-y=0的距离d=![]() ≤
≤![]() .
.
∴k≤-![]() 或k≥
或k≥![]() .
.
(2)令b=y-2x,则直线y=2x+b与圆x2+(y-2)2=3有公共点,
故圆心C(0,2)到直线2x-y+b=0的距离d=![]() ≤
≤![]() ,
,
∴2-![]() ≤b≤2+
≤b≤2+![]() .
.
评述:此题还可用“Δ”法,如(1)中,由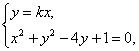
消y得(k2+1)x2-4kx+1=0有实数解.
令Δ=16k2-4(k2+1)≥0,
∴k2≥![]() .∴k≤-
.∴k≤-![]() 或k≥
或k≥![]() .
.

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目
已知实数x,y满足
-
=1(a>0,b>0),则下列不等式中恒成立的是( )
| x2 |
| a2 |
| y2 |
| b2 |
A、|y|<
| ||
B、y>-
| ||
C、|y|>-
| ||
D、y<
|