题目内容
(本小题满分12分)已知p:|1-
 |≤2,q:x2-2x+1-m2≤0(m>0),若
|≤2,q:x2-2x+1-m2≤0(m>0),若 p
p
是 q的必要而不充分条件,求实数m的取值范围.
q的必要而不充分条件,求实数m的取值范围.
解:由题意知,命题 若
若 p是
p是 q的必要而不充分条件的等价命题即逆否命题为:
q的必要而不充分条件的等价命题即逆否命题为:
p是q的充分不必要条件 ----------2分
----------2分
p:|1- |≤2
|≤2 -2≤
-2≤ -1≤2
-1≤2 -1≤
-1≤ ≤3
≤3 -2≤x≤10 -------4分
-2≤x≤10 -------4分
q::x2-2x+ 1-m2≤0
1-m2≤0 [x-(1-m)][x-(1+m)]≤0 ----------6分
[x-(1-m)][x-(1+m)]≤0 ----------6分
∵p是q的充分不必要条件,
∴不等式|1- |≤2的解集是x2-2x+1-m2≤0(m>0)解集的子集
|≤2的解集是x2-2x+1-m2≤0(m>0)解集的子集 --------8分
--------8分
又∵m>0 ∴不等式*的解集为1-m≤x≤1+m
∴不等式*的解集为1-m≤x≤1+m
∴ ,∴m≥9,
,∴m≥9,
∴实数m的取值范围是[ 9,+∞
9,+∞

 --------------12分
--------------12分
解析

练习册系列答案
相关题目
已知函数 ,定义如下:当
,定义如下:当 时,
时, ( ).
( ).
| A.有最大值1,无最小值 | B.有最小值0,无最大值 |
| C.有最小值—1,无最大值 | D.无最小值,也无最大值 |
 :
: 和条件
和条件 :
: ,请选取适当的实数
,请选取适当的实数 的值,分别利用所给的两个条件作为
的值,分别利用所给的两个条件作为 、
、 构造命题“若
构造命题“若 +2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围.
+2ax+2-a=0”,若命题“p且q”是真命题,求实数a的取值范围. 的定义域为R;命题q:
的定义域为R;命题q: 对一切的实数均成立,如果命题“p或q”为真命题,且“p且q”为假命题,求实数a的取值范围。
对一切的实数均成立,如果命题“p或q”为真命题,且“p且q”为假命题,求实数a的取值范围。 表示双曲线,命题q:点(
表示双曲线,命题q:点( ,
, )在圆
)在圆 的内部. 若
的内部. 若 为假命题,
为假命题, 也为假命题,求实数
也为假命题,求实数 的取值范围
的取值范围 :关于
:关于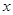 的不等式
的不等式 ,对一切
,对一切 恒成立,命题
恒成立,命题 :函数
:函数 是增函数,若
是增函数,若 为真,
为真, 为假,求实数
为假,求实数 的取值范围.
的取值范围. ,q:
,q:  (m>0),若
(m>0),若 是
是 的充分而不必要条件,求实数m的取值范围..
的充分而不必要条件,求实数m的取值范围..