题目内容

已知抛物线y²=2px（p＞0）的焦点为F，准线方程是 $数学公式$ ．
（1）求抛物线的方程；
（2）设点P在抛物线上，且|PF|=2，若O为坐标原点，求△OFP的面积．

解：（1）因为抛物线y²=2px（p＞0）的焦点为F，准线方程是 $\text{[math]}$ ．
∴p=1
∴抛物线的方程为：y²=2x．
（2）设P（x，y），点P在抛物线上，且|PF|=2，
由抛物线的定义得：x-（- $\text{[math]}$ ）=2，∴x= $\text{[math]}$ ，
将x= $\text{[math]}$ ，代入y²=2x得|y|= $\text{[math]}$ ，
则△OFP的面积S= $\text{[math]}$ |OF||y|= $\text{[math]}$ ．
分析：（1）利用抛物线的简单性质得出：抛物线准线与y轴的距离为 $\text{[math]}$ ，所以p=4最后写出抛物线的方程即可；
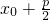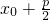（2）先设P（x，y），，将其代入抛物线的方程，求出x，再利用抛物线的定义得到点P到抛物线焦点的距离为 $\text{[math]}$ 求得|y|，最后利用三角形面积公式求解即可．．
点评：本小题主要考查抛物线的标准方程、抛物线的简单性质等基础知识，考查运算求解能力，考查数形结合思想．属于基础题．

练习册系列答案

天利38套新课标全国中考试题精选系列答案

中考试题研究满分特训方案系列答案

中考总复习名师A计划系列答案

百题大过关系列答案

考向标初中毕业学业考试指导系列答案

初中复习指导系列答案

发现中考系列答案

高考总复习优化方案系列答案

山西新中考系列答案

中考精确制导系列答案

相关题目

已知抛物线y²=2px（p＞0）．过动点M（a，0）且斜率为1的直线l与该抛物线交于不同的两点A、B，|AB|≤2p．
（1）求a的取值范围；
（2）若线段AB的垂直平分线交x轴于点N，求△NAB面积的最大值．

已知抛物线y²=2px（p＞0）的焦点为F，准线为l．
（1）求抛物线上任意一点Q到定点N（2p，0）的最近距离；
（2）过点F作一直线与抛物线相交于A，B两点，并在准线l上任取一点M，当M不在x轴上时，证明：

是一个定值，并求出这个值．（其中k_MA，k_MB，k_MF分别表示直线MA，MB，MF的斜率）

已知抛物线y²=2px（p＞0）．过动点M（a，0）且斜率为1的直线l与该抛物线交于不同的两点A、B，|AB|≤2p．求a的取值范围．

（2009•聊城一模）已知抛物线y²=2px（p＞0），过点M（2p，0）的直线与抛物线相交于A，B，

已知抛物线y²=2px（p＞0），M（2p，0），A、B是抛物线上的两点．求证：直线AB经过点M的充要条件是OA⊥OB，其中O是坐标原点．