题目内容
在平面直角坐标系xOy中,点A(-1,-2)、B(2,3)、C(-2,-1).(1)求以线段AB、AC为邻边的平行四边形两条对角线的长;
(2)设实数t满足(
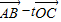 )•
)•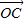 =0,求t的值.
=0,求t的值.
【答案】分析:(1)(方法一)由题设知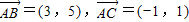 ,则
,则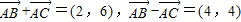 .
.
从而得: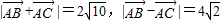 .
.
(方法二)设该平行四边形的第四个顶点为D,两条对角线的交点为E,则:
由E是AC,BD的中点,易得D(1,4)
从而得:BC=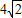 、AD=
、AD=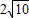 ;
;
(2)由题设知: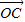 =(-2,-1),
=(-2,-1),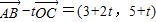 .
.
由(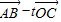 )•
)•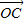 =0,得:(3+2t,5+t)•(-2,-1)=0,
=0,得:(3+2t,5+t)•(-2,-1)=0,
从而得: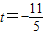 .
.
或者由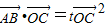 ,
,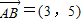 ,得:
,得: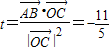
解答:解:(1)(方法一)由题设知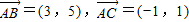 ,则
,则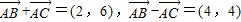 .
.
所以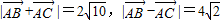 .
.
故所求的两条对角线的长分别为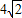 、
、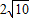 .
.
(方法二)设该平行四边形的第四个顶点为D,两条对角线的交点为E,则:
E为B、C的中点,E(0,1)
又E(0,1)为A、D的中点,所以D(1,4)
故所求的两条对角线的长分别为BC=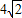 、AD=
、AD=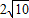 ;
;
(2)由题设知: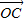 =(-2,-1),
=(-2,-1),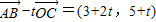 .
.
由(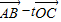 )•
)•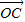 =0,得:(3+2t,5+t)•(-2,-1)=0,
=0,得:(3+2t,5+t)•(-2,-1)=0,
从而5t=-11,所以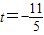 .
.
或者: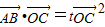 ,
,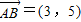 ,
,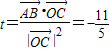
点评:本题考查平面向量的几何意义、线性运算、数量积,考查向量的坐标运算和基本的求解能力.
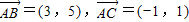 ,则
,则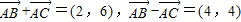 .
.从而得:
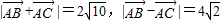 .
.(方法二)设该平行四边形的第四个顶点为D,两条对角线的交点为E,则:
由E是AC,BD的中点,易得D(1,4)
从而得:BC=
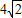 、AD=
、AD=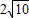 ;
;(2)由题设知:
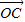 =(-2,-1),
=(-2,-1),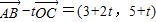 .
.由(
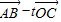 )•
)•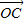 =0,得:(3+2t,5+t)•(-2,-1)=0,
=0,得:(3+2t,5+t)•(-2,-1)=0,从而得:
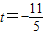 .
.或者由
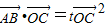 ,
,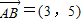 ,得:
,得: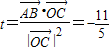
解答:解:(1)(方法一)由题设知
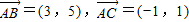 ,则
,则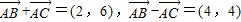 .
.所以
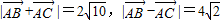 .
.故所求的两条对角线的长分别为
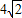 、
、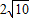 .
.(方法二)设该平行四边形的第四个顶点为D,两条对角线的交点为E,则:
E为B、C的中点,E(0,1)
又E(0,1)为A、D的中点,所以D(1,4)
故所求的两条对角线的长分别为BC=
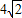 、AD=
、AD=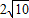 ;
;(2)由题设知:
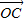 =(-2,-1),
=(-2,-1),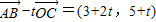 .
.由(
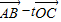 )•
)•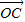 =0,得:(3+2t,5+t)•(-2,-1)=0,
=0,得:(3+2t,5+t)•(-2,-1)=0,从而5t=-11,所以
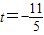 .
.或者:
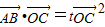 ,
,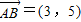 ,
,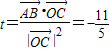
点评:本题考查平面向量的几何意义、线性运算、数量积,考查向量的坐标运算和基本的求解能力.

练习册系列答案
 小学课时特训系列答案
小学课时特训系列答案
相关题目
 如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是
如图,在平面直角坐标系xOy中,锐角α和钝角β的终边分别与单位圆交于A,B两点.若点A的横坐标是