Question

如图，三棱锥P-ABC中，PA=a，AB=AC=2a，∠PAB=∠PAC=∠BAC=60°，求三棱锥P-ABC的体积．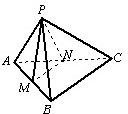

Answer 1

分析：由题中数量关系知，取底面△ABC的边AB、AC的中点M、N，得棱长为a的正四面体P-AMN，求出它的体积，
三棱锥P-ABC的体积=4×三棱锥P-AMN的体积，从而求出体积．

解答：解：如图，取AB、AC的中点M、N，连接PM，PN，MN，
则PA=AM=AN=a，由∠PAB=∠PAC=∠BAC=60°，
得：PM=PN=MN=a，∴三棱锥P-AMN是棱长为a的正四面体，它的体积为，
V_P-AMN=

1

3

•S_△AMN•h=

1

3

×

1

2

×a²×sin60°×

a2 -( 2 3 ×  3 2 a)2

=

2

12

a³；
三棱锥P-ABC的体积为，V_P-ABC=

1

3

•S_△ABC•h=

1

3

×4•S_△AMN•h=4V_P-AMN=

2

3

a3．

点评：本题通过转化为正四面体，由正四面体的体积，求得锥体的体积，是一种很好的求体积的方法．