题目内容
已知直线ax-by-2=0与曲线y=x3-lnx在点p(1,1)处的切线互相垂直,则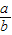 为 .
为 .
【答案】分析:先求出曲线y=x3-lnx在点p(1,1)处的切线斜率,根据直线和切线垂直建立方程关系,即可求解.
解答:解:曲线y=x3-lnx的导数为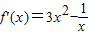 ,则当x=1时,f'(1)=3-1=2,即切线的斜率k=2,
,则当x=1时,f'(1)=3-1=2,即切线的斜率k=2,
因为直线ax-by-2=0点p(1,1)处的切线互相垂直,所以直线ax-by-2=0为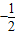 .
.
即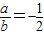 ,所以
,所以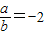 .
.
故答案为:-2.
点评:本题主要考查导数的几何意义以及直线垂直的关系的应用,利用导数求切线斜率是解决本题的关键.
解答:解:曲线y=x3-lnx的导数为
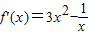 ,则当x=1时,f'(1)=3-1=2,即切线的斜率k=2,
,则当x=1时,f'(1)=3-1=2,即切线的斜率k=2,因为直线ax-by-2=0点p(1,1)处的切线互相垂直,所以直线ax-by-2=0为
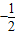 .
.即
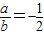 ,所以
,所以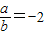 .
.故答案为:-2.
点评:本题主要考查导数的几何意义以及直线垂直的关系的应用,利用导数求切线斜率是解决本题的关键.

练习册系列答案
相关题目
已知直线Ax+By+C=0(其中A2+B2=C2,C≠0)与圆x2+y2=4交于M,N,O是坐标原点,则
•
=( )
| OM |
| ON |
| A、-1 | B、-1 | C、-2 | D、2 |