题目内容
△ABC中,已知tanA= ,tanB=
,tanB= ,则∠C等于
,则∠C等于
- A.30°
- B.45°
- C.60°
- D.135°
D
分析:由三角形的内角和定理得到C=π-(A+B),可得出tanC=tan[π-(A+B)],利用诱导公式化简等式的右边后,再利用两角和与差的正切函数公式化简,将tanA和tanB的值代入求出-tan(A+B)的值,即为tanC的值,由C为三角形的内角,利用特殊角的三角函数值即可求出C的度数.
解答:∵tanA= ,tanB=
,tanB= ,
,
∴tanC=tan[π-(A+B)]=-tan(A+B)=-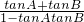 =-
=- =-1,
=-1,
又C为三角形的内角,
则C=135°.
故选D
点评:此题考查了诱导公式,两角和与差的正切函数公式,以及特殊角的三角函数值,熟练掌握公式是解本题的关键.
分析:由三角形的内角和定理得到C=π-(A+B),可得出tanC=tan[π-(A+B)],利用诱导公式化简等式的右边后,再利用两角和与差的正切函数公式化简,将tanA和tanB的值代入求出-tan(A+B)的值,即为tanC的值,由C为三角形的内角,利用特殊角的三角函数值即可求出C的度数.
解答:∵tanA=
 ,tanB=
,tanB= ,
,∴tanC=tan[π-(A+B)]=-tan(A+B)=-
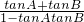 =-
=- =-1,
=-1,又C为三角形的内角,
则C=135°.
故选D
点评:此题考查了诱导公式,两角和与差的正切函数公式,以及特殊角的三角函数值,熟练掌握公式是解本题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
 ;
; (注:
(注: 表示△ABC的面积)
表示△ABC的面积) ;
; (注:
(注: 表示△ABC的面积)
表示△ABC的面积)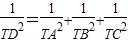 ;
; (注:S△ABC表示△ABC的面积)
(注:S△ABC表示△ABC的面积) ;
; (注:S△ABC表示△ABC的面积)
(注:S△ABC表示△ABC的面积)