题目内容
在△ABC中，
，则过点C，以A，H为两焦点的椭圆的离心率为 ．
【答案】分析：由题意可得
=
，由AH⊥BC可得，
，根据椭圆的定义可得，2a=CA+CH，2c=AH
，根据
可求
解答：解：由题意可得
=
∵
∴AH⊥BC
在Rt△AHC中可得，
故可设CH=3x，则可得AH=4x，AC=5x
根据椭圆的定义可得，2a=CA+CH=8x，2c=AH=4x
∴
=
=
故答案为：
．
点评：本题主要考查了椭圆定义及离心率的求解，解题的关键是根据二倍角的正切公式先求tanC，关键二是要灵活应用椭圆的定义得到，2a=CA+CH，2c=AH．
=，由AH⊥BC可得，，根据椭圆的定义可得，2a=CA+CH，2c=AH，根据
可求解答：解：由题意可得
=∵
∴AH⊥BC在Rt△AHC中可得，
故可设CH=3x，则可得AH=4x，AC=5x
根据椭圆的定义可得，2a=CA+CH=8x，2c=AH=4x
∴
==故答案为：
．点评：本题主要考查了椭圆定义及离心率的求解，解题的关键是根据二倍角的正切公式先求tanC，关键二是要灵活应用椭圆的定义得到，2a=CA+CH，2c=AH．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
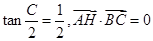，则过点C，以A、H为焦点的双曲线的离心率为 （ ）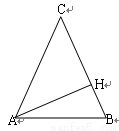
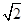D．
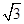
，则过点C，以A，H为两焦点的椭圆的离心率为 ．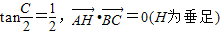
，则过点C，以A，H为两焦点的椭圆的离心率为 ．
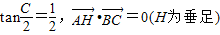，则过点C，以A，H为两焦点的椭圆的离心率为 ．